Miary kątów w trapezie
Zdolny_Rudek: Uzasadnij, że w trapezie suma miar kątów wewnętrznych leżących przy jednym ramieniu jest równa
180*
Proszę o dokładne wytłumaczenie gdyż moja matematyczka bardzo dużo wymaga i nie zadowoli ją
jedno zdanie, a także proszę o dobrze opisany obrazek trapezu.
Z góry dzięki wszystkim.
3 cze 18:13
Eta:

3 cze 18:15
bezendu: 
3 cze 18:16
Zdolny_Rudek: ha.Ha. Czyli nikt nie odpowie ?
3 cze 18:17
5-latek : Skorzystaj z twierdzenia ze suma katow przyleglych lezacych na jednym ramieniu wynosi 180
stopni.
3 cze 18:19
Zdolny_Rudek: Weźcie, odpowie ktoś



Potrzebuje tego na CITO.
3 cze 18:20
Zdolny_Rudek: Dzięki ale to za mało. Jakiś rysunek trapezu, coś ładnie, wiecie tak fajnie [jakbyś całował
dziewczynę]
3 cze 18:21
Eta:
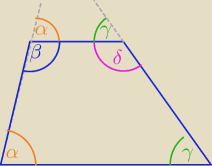
3 cze 18:24
Eta:
No to teraz "całuj" obrazek do zeszytu

3 cze 18:25
Zdolny_Rudek: Och dziękuję

Ale jeszcze jakieś kilka słów komentarza [czyli teraz, dowód,] takie bajery
3 cze 18:26
Zdolny_Rudek: Wiesz a całowaniem jest jak z pisaniem książki, jak idzie to idzie ale jak sie jeb** to po
całości. A zeszytu nie będe całować tylko ciebie w policzek za rozwiązanie.
3 cze 18:28
Mauo_Zdolny_Rudek: A mogę liczyć na jakis opis sensowny do tego rysunku ?
3 cze 18:30
Mauo_Zdolny_Rudek: Halo !
3 cze 18:37
PW: To nie ma zbyt wiele wspólnego z trapezem. Ważne, że są dwie proste równoległe przecięte
trzecią prostą (i taki rysunek wystarczy; domagałeś się, więc Eta z dobroci serca
wykonała taki jak chciałeś).
A dowód, że α=β wynika np. z własności symetrii środkowej. Bierzemy punkt S środek ramienia
trapezu. W symetrii o środku S ramię przekształca się na siebie. Proste zawierające podstawy
trapezu przekształcają się na proste do nich równoległe, przechodzące przez wierzchołki
trapezu. Z pewnika geometrii euklidesowej (przez punkt leżący poza prostą przechodzi tylko
jedna prosta do niej równoległa) wynika w takim razie, że obrazem prostej zawierającej jedną z
podstaw jest prosta zawierająca drugą podstawę (i na odwrót). Tym samym kąty utworzone przez
ramię trapezu i jedną z półprostych zawierających podstawę mają ramiona równoległe. To zaś
oznacza, że są albo przystające, albo dopełniające. Jeszcze tylko dlaczego nie są przystające
i koniec dowodu.
Rzeczywiście jakby całował dziewczynę. Uważaj, żebyś z tego zachwytu nie zapragnął zostać
matematykiem − gwarantuję że to wciąga.
3 cze 18:49
PW: PS
Trochę się wygłupiam − to że mają ramiona równoległe to widać (definicja trapezu).
3 cze 18:51
5-latek : Albo mozna tez udowodnic ze jesli dwie proste rownolegle zostaly przeciete sieczna to suma
katow jednostronnie wewnetrznych jest rowna 180 stopni . Nie narysuje bo nie umiem tu rysowac.
3 cze 19:19
BARTEK: To się naucz to proste nawet 5−latek dałby sobie radę
3 cze 19:25
PW: @BARTEK: Nic mnie bardziej nie irytuje jak próby rysowania w tym edytorze, to się samo rządzi i
nigdy nie udało mi się osiągnąć zamierzonego celu. Jest nas w takim razie już dwóch z
5−latkiem.
3 cze 19:29
5-latek : Bartku ja juz jestem za stary na to Naprawde .

.
3 cze 19:31
5-latek : Pozdrawiam Ciebie PW
3 cze 19:33
5-latek : Bartek .A zadanie z ciagiem zrobiles ?
3 cze 19:35
Eta:

3 cze 19:38
3 cze 19:42
5-latek : ETA bardzo ladny rysunek . Pozdrawiam i

3 cze 19:45
Eta:
Hehe ......... aja już drugi dzień myślę ..... kim jest
5−latek :=

pozdrawiam i z okazji
Dnia Dziecka 
3 cze 19:47
Kostek: @Eta ale dzień dziecka już był

3 cze 19:48
Eta:
Prezenty są miłe ..........z okazji i nawet bez ....

3 cze 19:50
PW: Ale widzisz, Eta, muszka nie jest symetryczna. Mnie takie rzeczy irytują (trochę
pracowałem w poligrafii, gdzie wymaga się perfekcyjnego projektu), więc w ogóle z rysowania
rezygnuję. Marzy mi się, żeby można było rysunek wykonany "w czym innym" przekonwertować np.
na *.eps i wstawić tutaj.
3 cze 19:50
Mauo_Zdolny_Rudek: Dzięki wam

Wszystkim ! Nawet tym którzy przyszli sie pośmiać. Pozdrawia was
Mauo
Zdolny
Rudek
3 cze 20:02




 Potrzebuje tego na CITO.
Potrzebuje tego na CITO.


 Ale jeszcze jakieś kilka słów komentarza [czyli teraz, dowód,] takie bajery
Ale jeszcze jakieś kilka słów komentarza [czyli teraz, dowód,] takie bajery
 .
.


 pozdrawiam i z okazji Dnia Dziecka
pozdrawiam i z okazji Dnia Dziecka 


 Wszystkim ! Nawet tym którzy przyszli sie pośmiać. Pozdrawia was
MauoZdolnyRudek
Wszystkim ! Nawet tym którzy przyszli sie pośmiać. Pozdrawia was
MauoZdolnyRudek