FUNKCJE TRYGONOMETRYCZNE
olkaq:
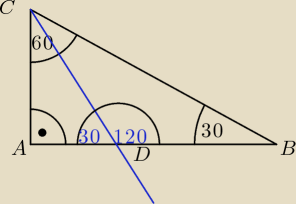
W trójkącie prostokątnym ABC, kąt przy wierzchołku A jest prosty, zaś |∡ACB| = 60. Dwusieczna
kąta ACB przecina bok AB w punkcie D. Wykaż, że:
|CB|
2 − 2 * |DB|
2 = |AD|
2 + |AC|
2
1 cze 12:35
Nienor: A kąty skąd

(te na niebiesko). Przecież to nie możliwe

Z tw. Pitagorasa:
|CB|
2=|AC|
2+(|AD|+|DB|)
2
|CB|
2=|AC|
2+|AD|
2+2|AD||DB|+|DB|
2
Zauważ, że |AD|=|DB|
1 cze 12:42
THIRTEEN [13]: W twoim rysunku powinnaś zmienić tylk miarę tego kąta
30 na 60

Ogólnie rysunek jest dobry jak do tego zadania
1 cze 12:46
THIRTEEN [13]: Mnienmam że kąt ACB ma 60 stopni czyli jego dwusieczna dzieli go na dwa kąty 30 stopni i 30
stopni
1 cze 12:49
1 cze 13:24
1 cze 13:29
BARTEK:
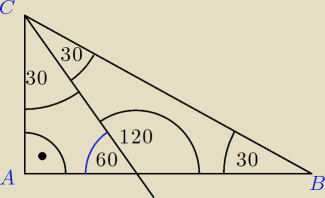
Zadanie jest proste wystarczy tylko rozpisać zależności
1 cze 13:34
olkaq: Czy mógłby ktoś podać rozwiązanie bo chciałabym sobie to sprawdzić, a w zbiorze nie mam
odpowiedzi do tego zadania.
2 cze 15:28
 W trójkącie prostokątnym ABC, kąt przy wierzchołku A jest prosty, zaś |∡ACB| = 60. Dwusieczna
kąta ACB przecina bok AB w punkcie D. Wykaż, że:
|CB|2 − 2 * |DB|2 = |AD|2 + |AC|2
W trójkącie prostokątnym ABC, kąt przy wierzchołku A jest prosty, zaś |∡ACB| = 60. Dwusieczna
kąta ACB przecina bok AB w punkcie D. Wykaż, że:
|CB|2 − 2 * |DB|2 = |AD|2 + |AC|2
 (te na niebiesko). Przecież to nie możliwe
(te na niebiesko). Przecież to nie możliwe  Z tw. Pitagorasa:
|CB|2=|AC|2+(|AD|+|DB|)2
|CB|2=|AC|2+|AD|2+2|AD||DB|+|DB|2
Zauważ, że |AD|=|DB|
Z tw. Pitagorasa:
|CB|2=|AC|2+(|AD|+|DB|)2
|CB|2=|AC|2+|AD|2+2|AD||DB|+|DB|2
Zauważ, że |AD|=|DB|
 Ogólnie rysunek jest dobry jak do tego zadania
Ogólnie rysunek jest dobry jak do tego zadania





 Zadanie jest proste wystarczy tylko rozpisać zależności
Zadanie jest proste wystarczy tylko rozpisać zależności