27 maj 16:45
janusz: Proszę o pomoc, jutro mam sprawdzian z tego −.−
27 maj 17:17
Eta:
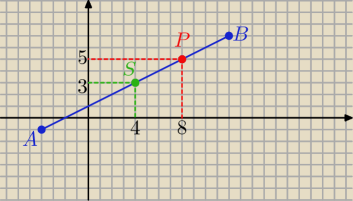
Skoro bez wektorów, to:
| | 12−4 | | 7−1 | |
z podziału odcinka AB na połowę : S( |
| . |
| ) = S(4,3) |
| | 2 | | 2 | |
i jeszcze raz odcinek SB na połowę :
| | 12+4 | | 7+3 | |
P( |
| , |
| )=P (8,5) |
| | 2 | | 2 | |
27 maj 17:31
Eta:
27 maj 17:34
janusz: Dzięki bardzo. Zacząłem robić 7 na podstawie podobnego z neta, ale dziwne wyniki. Dasz radę
rozpisać do końca to 7?
27 maj 17:49
Eta:
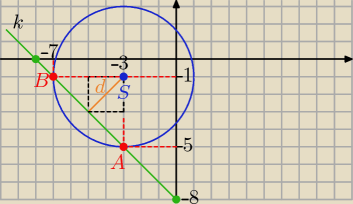
o: x
2+y
2+6x+2y=0 , S( −3, −1) , r=
√10
k: x+y+8=0
| | |−3−1+8| | | 4 | |
d= |
| = |
| = 2√2 |
| | √2 | | √2 | |
punkty wspólne prostej k i okręgu wyznaczamy rozwiązując układ równań:
y= −x−8
x
2+y
2+6x+2y=0 ⇒ x
2+(−x−8)
2+6x+2(−x−8)=0
x
2+x
2+16x+64+6x−2x−16=0 ⇒ x
2+10x+48=0 ,Δ= 4
x= −3 v x= −7 to y= −5 v y= −1
A( −3, −5) , B( −7, −1)
27 maj 18:22
janusz: Dziękuje Ci za pomoc
Dotarłem do momentu 2√2 i właśnie nie wiedziałem jak wyznaczyć wspólne
punkty.
27 maj 18:23
27 maj 18:24
27 maj 18:24
Eta:
Na zdrowie ..
i powodzenia na sprawdzianie
27 maj 18:26
janusz: Jeszcze jedno
Tutaj powinno być 24 zamiast 48
"⇒ x2+10x+48=0 ,Δ= 4"
Skoro √Δ=2 to
x1=(−10−2)/2=−6
x2=(−10+2)/2=−4
y1=−(−6)−8=−2
y2=−(−4)−8=−4
Coś zgubiłem czy tam jest błąd jednak?
27 maj 18:47
Eta:
Jasne,że : x
2+10x+
24=0 Δ=100−96= 4
dalej jest ok
widać choćby na rys.
27 maj 18:49
janusz: Kurde to ja nie wiem czemu miejsca zerowe wyszły Ci −3 i −7, możesz to rozpisać? Bo ja właśnie
sobie sam pisałem i mi wyszło tak jak powyżej.
27 maj 18:54
Eta:
Masz 100% racji ( boli mnie głowa i dlatego zamiast
√Δ=2 wpisałam 4
| | −10+2 | | −10−2 | |
x= |
| = −4 v x= |
| = −6 |
| | 2 | | 2 | |
to y= 4−8= −4 v y= 6−8= −2
A(−4, −4) , B( −6, −2)
A na rysunku też popraw ( bo widzę,że promień r zamiast
√10 dałam r= 4
Przepraszam
27 maj 19:02
janusz: Nie mam doświadczenia w tym rysowniku
a muszę się właśnie pouczyć jeszcze
Ktoś jak przeczyta wszystko to zobaczy poprawne odpowiedzi.
Tak czy siak dziękuje za pomoc. Pozdro
27 maj 19:18
