Funkcja kwadratowa Olga: Dla jakich wartości parametru m równanie (2−m)x²+(3−m)x+1=0 ma dwa różne pierwiastki ujemne?

bezendu: rozważ przypadki Δ>0 x₁*x₂>0

bezendu: i jeszcze m≠2

krystek: I jeszcze x₁+x₂<0

Olga: Rozważyłam te przypadki. a≠0 ⇒ 2−m≠0, czyli m≠2 Wyszło mi, że Δ=m²−2m+1>0 a Δ₁=4−4=0

	−b		2
miejsce zerowe=		=		=1 i teraz rysujemy to na wykresie a>0, a Δ=0, dlatego
	2a		2

m∊(−∞,1)u(1,∞)

	−b		m−3
Póżniej x1+x2=				<0/ x(2−m) m−3<0 m<0
	a		2−m

	c		1
x1x2=				>0/ x(2−m) 1>0 x∊R
	a		2−m

No i na końcu uwzględniam to wszystko i mi wychodzi, że m∊(−∞,1)u(1,2)u(2,3) Mam błąd, tylko nie wiem, gdzie. W odpowiedziach jest napisane, że m∊(−∞,1)u(1,2)

krystek: Nierówności wymiernej nie mnozysz przez mianownik !

krystek:

m−3
	<0⇔(m−3)(2−m)<0⇔m∊..
2−m

Olga: Dzięki tym wykrzyknikom zapamiętam to do końca życia. Dziękuję bardzo

Olga: no i z tego wyjdą miejsca zerowe 3 i 2 i potem na wykresie wychodzi, że m∊(2,3), a tej trójki nie ma w odpowiedzi. Znów mi coś nie wyszło

krystek:

	1
I jeszcze		>0⇔2−m>0⇔m<2
	2−m

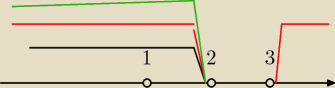
krystek: odp x∊(−∞,2)/{1}

Olga: no i wtedy mamy, że m∊(−∞,1)u(1;∞) m∊(2,3) m<2 no i wtedy to sumujemy i wychodzi, że m∊(−∞,1)u(1,2)u(2,3) a w odp. jest bez tego (2,3)

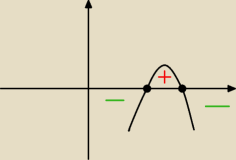
krystek: @Olga (m−3)(2−m)<0⇔m∊(−∞,2)U(3,∞)

krystek:

Olga: Dlaczego będzie w (m−3)(2−m)<0 że m∊(−∞,2)u(3,∞) a nie m∊(2,3)?

Olga: No właśnie, dlaczego parabola ma ramiona skierowane do dołu? Przecież przed (m−3)(2−m) nie ma minusa

krystek: −m² gałęzie w dół

krystek: ale m*(−m)=−m²

Olga: Ok już rozumiem. Bardzo dziękuję

krystek: Poćwicz rozwiązywanie nierówności !

krystek: https://matematykaszkolna.pl/strona/1696.html

krystek: https://matematykaszkolna.pl/strona/93.html