nierówości
matematyk: Rozwiąż nierówności:
1.|x
2−2x|<x
2.|3x−x
2)<2−x

?
25 maj 22:05
25 maj 22:43
Mila:
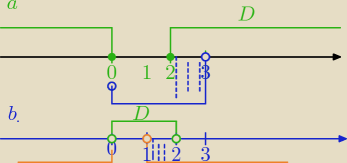
1) |x
2−2x|<x
a)
|x
2−2x|=x
2−2x⇔x
2−2x≥0⇔x(x−2)≥0⇔
x≤0 lub x≥2 na osi
wtedy mamy nierówność:
D=(−
∞,0>∪<2,
∞)
x
2−2x<x⇔x
2−3x<0⇔x(x−3)<0⇔
x∊(0,3)
x∊<2,3)
b)
D=(0,2)
|x
2−2x|=−x
2+2x
wtedy mamy nierówność:
−x
2+2x<x⇔−x
2+x<0⇔x(−x+1)<0⇔x<0 lub x>1
x∊(1,2)
łącznie:x∊(1,3)
25 maj 23:01
pigor: ..., lub inaczej
1)
|x2−2x| < x ⇒ dla x≤ 0 jest to nierówność sprzeczna, a dla x >0 jest ⇔
⇔ x|x−2|< x / : x >0 ⇔ |x−2|< 1 ⇔ −1< x−2< 1 /+2 ⇔ 1< x < 3 ⇔
x∊(1;3) . ...

25 maj 23:57
pigor: ..., a
2)
|3x−x2|< 2−x ma sens ⇔ 2−x >0 ⇔
(*) x<2 i x−2 < 3x−x
2 <2−x ⇔
⇔ x
2−2x−2< 0 i x
2−4x+2 >0 ⇔ x
2−2x+1−3< 0 i x
2−4x+4−2 >0 ⇔
⇔ (x−1)
2< 3 i (x−2)
2>2 ⇔ |x−1|<
√3 i |x−2| >
√2 ⇔
⇔ −
√3< x−1<
√3 i (x−2< −
√2 lub x−2>
√2) ⇔
⇔ −
√3+1< x < 1+
√3 i (x< 2−
√2 lub x >2+
√2) , to stąd i z
(*) ⇔
⇔
2−√2 < x < 2 ⇔
x∊(2−√2 ; 2) − szukany
zbiór rozwiązań . ...

26 maj 00:18
Eta:
Ach jak piknie
 kolorowo
kolorowo 
26 maj 00:34
Basia: pierwsze można trochę uprościć
|x2−2x| < x
dla x≤0 nie ma rozwiązania bo |...| nie może być mniejsza ani od liczby ujemnej, ani od 0
dla x>0 mamy
|x2−2x| = |x(x−2)| = |x|*|x−2| = x*|x−2|
czyli mamy nierówność
x*|x−2| < x i x>0
dzielimy przez x
|x−2| < 1
−1 < x−2 < 1
1 < x < 3
26 maj 11:52
 ?
?
 1) |x2−2x|<x
a)
|x2−2x|=x2−2x⇔x2−2x≥0⇔x(x−2)≥0⇔x≤0 lub x≥2 na osi
wtedy mamy nierówność:
D=(−∞,0>∪<2,∞)
x2−2x<x⇔x2−3x<0⇔x(x−3)<0⇔x∊(0,3)
x∊<2,3)
b)
D=(0,2)
|x2−2x|=−x2+2x
wtedy mamy nierówność:
−x2+2x<x⇔−x2+x<0⇔x(−x+1)<0⇔x<0 lub x>1
x∊(1,2)
łącznie:x∊(1,3)
1) |x2−2x|<x
a)
|x2−2x|=x2−2x⇔x2−2x≥0⇔x(x−2)≥0⇔x≤0 lub x≥2 na osi
wtedy mamy nierówność:
D=(−∞,0>∪<2,∞)
x2−2x<x⇔x2−3x<0⇔x(x−3)<0⇔x∊(0,3)
x∊<2,3)
b)
D=(0,2)
|x2−2x|=−x2+2x
wtedy mamy nierówność:
−x2+2x<x⇔−x2+x<0⇔x(−x+1)<0⇔x<0 lub x>1
x∊(1,2)
łącznie:x∊(1,3)


 kolorowo
kolorowo 