Wielomiany. pablo: Udowodnij, że wielomian f(x)=x⁶−x⁵+x⁴−x³+x²−x+³₄ nie ma pierwiastków rzeczywistych.

asdf: umiesz pochodne?

pablo: nie ;c

Dominik: asdf, jak to rozwiazac z wykorzystaniem pochodnych? z policzeniem pochodnej wielomianu nie mam problemu.

Ajtek: Dominik przebieg zmienności funkcji i ognia.

asdf: policz ekstrema i sprawdź czy są nad OX

Ajtek: Cześć asdf .

asdf: hej

Dominik: policzenie f'(x) = 0 raczej nie bedzie zbyt przyjemne, chyba ze mam mylne pojecie o tym, jak sie liczy ekstrema. analize bede mial dopiero w pazdzierniku.

ICSP: a po co chcesz liczyć f'(x) = 0 ?

Ajtek: Dominik analizę zacznij już teraz . Będziesz miał łatwiej. Polecam Krysicki Włodarski "Analiza matematyczna w zadaniach"

Ajtek: Cześć ICSP .

asdf: już wiem jak to zrobić, nie trzeba pochodnych , podpowiedź:

3		1		1		1
	=		+		+
4		4		4		4

asdf: albo nie...taka lepsza:

	1		1
x2 − x +		= (x−		)2
	4		2

Dominik: ISCP, wydawalo mi sie, ze tak liczy sie ekstrema. przynajmniej dla funkcji kwadratowej to dziala. Ajtek, analiza wydaje mi sie latwa na tyle, ze ogarne ja bez bolu na studiach. teraz wole sie przygotowac z logiki i teorii mnogosci.

ICSP: i co Ci da tutaj ekstremum ? Będziesz wiedział gdzie jest i tyle (oczywiście o ile rozwiążesz równanie stopnia V )

Ajtek: Domikik powodzenia życzę .

asdf: @Dominik nie wiem czy analiza jest taka prosta Zalezy jaki masz sylabus i co potrafisz. Logika wydaje mi sie prostsza

Dominik: Ajtek, wielkie dzieki. ISCP, sugerowalem sie postem asdf z godz. 23:17. sposob wydaje mi sie sensowny, ale zasygnalizowalem juz wczesniej istote problemu rozwiazania rownania f'(x) = 0.

asdf: @ICSP zbadac kazde minimum ekstrema i sprawdzić czy jest dodatnie, mozna tak?

ICSP: za mało.

asdf: i przypadek drugi dla maximum, czy jest zawsze ujemne

asdf: ja lece, całki sie same nie policzą...

Dominik: asdf, jak mozesz to przejrzyj skrypt do podstaw matematyki na MIM UW. tutaj link: http://www.mimuw.edu.pl/~urzy/Pmat/pomat.pdf jesli chodzi o analize to jest tutaj http://wazniak.mimuw.edu.pl/index.php?title=Analiza_matematyczna_1 na 2 semestrze jest chyba analiza II.

asdf: jednak jest wiecej tych przypadkow, ale mam co innego na glowie

asdf: @Dominik to jest teoria....przykladowo − granice są niby proste..ale jak trafisz na trudny przyklad to mozesz z tym walczyc dlugo, tak w kazdym przedmiocie. Jak masz pol roku to mozesz spokojnie ogarnac etrapeza do całej nieoznaczonych (radze przejsc wedlug tamtej listy, wcześniej całek nie ruszać − a zwłaszcza jak nie znasz pochodnych − sie tylko zniechęcisz..) kiedy indziej moze pomoge (chociaz na forum sa lepsi, Triviala popytaj jezeli chodzi o zadania z kosmosu i logike)

ZKS:

	3
x4(x2 − x + 1) − x(x2 − x + 1) +		=
	4

	3
(x2 − x + 1)x(x − 1)(x2 + x + 1) +
	4

Pokażmy że to wyrażenie jest zawsze większe od zera

	3
(x2 − x + 1)x(x − 1)(x2 + x + 1) +		> 0
	4

wyrażenie (x² − x + 1)x(x − 1)(x² + x + 1)

	3
dla x ∊ (−∞ ; 0) ∪ (1 ; ∞) jest zawsze dodatnie tak więc po dodaniu		też będzie ta
	4

wartość dodatnia. Teraz należy jeszcze rozpatrzyć przypadek dla x ∊ [0 ; 1] sprawdzimy czy w tym przedziale znajduje się pierwiastek korzystając z twierdzenia Darboux

	3
f(0) =
	4

	3
f(1) =
	4

f(0) * f(1) > 0 tak więc w podanym przedziale nie ma pierwiastków rzeczywistych. Nie wiem czy takie udowodnienie może być. Pomyślę jeszcze później nad innym sposobem.

Ajtek: ZKS czapka zgłowy . A tak w ogóle to cześć .

ZKS: Witam Ajtuś jak to teraz na Ciebie się mówi.

Ajtek:

Mila: OOOO! Witaj Ajtek, ZKS, Dlaczego Ajtuś. I Dobranoc

Ajtek: Mila a tak wyszło tutaj 204337 Spokojnej nocy życzę .

teofrast: Po to, by móc skorzystać z twierdzenia Darboux, należałoby wykazać monotoniczność funkcji na przedziale [0, 1]. Kontrprzykład? Wystarczy wyobrazić sobie np. sinx w przedziale [90, 450 ] I co? Na krańcach przedziału mamy jedynki, a w środku są aż dwa zera...

ICSP: ZKS nie mogę się zgodzić. Twierdzenie Darboux mówi coś innego .

ZKS: Witaj Mila i Dobranoc.

teofrast: twierdzenie Darboux mówi, że jezeli wartości na krańcach przedziału róznego znaku, to funkcja ma w tym przedziale pierwiastek. Z tego nie wynika, że jeśli wartości na krańcach przedziału są lego samego znaku, to funkcja nie ma pierwiastka... Kontrprzykład j.w. Po prostu ( A⇒B)≠(¬A ⇒ ¬B)

ZKS: To trzeba pomyśleć.

ICSP:

	3		1		3		1
x6 − x5 + x4 − x3 + x2 − x +		=		x6 − x5 + x4 +		x6 − x3 +
	4		4		4		2

	1		1		1		3		1
+ x2 − x +		= (		x3 − x2)2 + (x −		)2 +		x6 − x3 +		=
	4		2		2		4		2

	1		1		√3		√3		1
= (		x3 − x2)2 + (x −		)2 + (		x3 −		)2 +
	2		2		2		3		6

komentarz i gotowe

Vizer: Wydaje mi się, że dałoby radę przy pomocy pochodnych to udowodnić. Bo jeżeli jest to wielomian gdzie najwyższym stopniem jest parzysta liczba i jest on o dodatnim współczynniku, to wystarczy sprawdzić czy jego minima są powyżej osi OX. Czy tutaj się to łatwo będzie liczyć, tego nie wiem bo nie próbowałem.

pigor: ... , np. tak : f(x)= x⁶−x⁵+x⁴−x³+x²−x+³₄= x⁵(x−1)+x³(x−1)+x(x−1)+³₄= = (x−1)(x⁵+x³+x)+³₄= x(x−1)(x⁴+x²+1)+³₄ >0, bo x(x−1)∊(−¹₂;+∞) ∀x∊R

ZKS:

	3
Jeżeli zamiast		było by 1 to zadanie w 1 minutę roboty bo mam fajny sposób.
	4

pigor: ..., przepraszam , g(x)=x(x−1) > g(¹₂)= −¹₄ , czyli x(x−1)∊(−¹₄;+∞). ...

ZKS: ICSP heh trochę trzeba było pomyśleć aby to wykombinować.

teofrast: szacowanie iloczynu przez szacowanie czynników jest sprawą delikatną, gdy w grę wchodzą liczby ujemne: Prawdą jest, że x⁴ + x² + 1 > 1 & x(x−1) ≥ −1/4 . Ale z tego nie wynika że iloczyn tych dwóch wielomianów na pewno jest ≥ −1/4. Wystarczy sobie wyplotować rzeczony iloczyn, by zobaczyć, że jest on > ca. (−0.37). W rzeczywistości na przedziale [0, 1] drugi z tych czynników jest zawsze ujemny, przeto nie można mnożyć stronami obydwu nierówności...

asdf: Ok, zrobiłem, nie pytajcie skąd wziąłem ten wynik − 4 strony A4 grupowania... http://www.wolframalpha.com/input/?i=x%5E6+-+x%5E5+%2B+x%5E4+-+x%5E3+%2B+x%5E2+-+x+%2B+3%2F4+%3D+%28x%5E2+-+x%29%28%28x%5E2-1%2F4%29%5E2+%2B+3%2F4%282x%5E2%2B5%2F4%29%29+%2B3%2F4 przepisałem jakby komuś się nie chciało wchodzić (z wolframa) :

	1		3		5		3
(x2−x)((x2−		)2 +		(2x2 +		) ) +
	4		4		4		4

komentarz:

	−1
x2−x >		zawsze
	4

asdf: oczywiście chodziło mi, że:

	1
f(x) > −		oczywiście..co łatwo udowodnić, z resztą − pigor ma podobne rozwiązanie wiec
	4

nie bede sie rozpisywać

teofrast: vide moja poprzednia uwaga...rozumowanie asdf' a i pigora są błędne... ( ze względu na to nieszczęsne oszacowanie > −1/4 )

asdf:

	1
x2−x +		≥ 0
	4

	1
(x−		)2 ≥ 0
	2

asdf: a no tak masz rację

teofrast: Niemniej powyższe rozumowania można uratować: 1) z tw. Kartezjusza wynika, że wielomian W(X) = P(x) + 3/4 nie ma pierwiastków ujemnych; 2) x(1−x)(x⁴ + x² + 1) + 3/4 przyjmuje wartości dodatnie dla x spoza (0, 1) 3) Oszacujemy Z GÓRY wyrazenie − P(x) = x( x− 1) ( x⁴ + x² + 1) : W tym celu zauważmy, że x⁴ + x² + 1 jest ściśle rosnąca na (0, 1) i wartość największą osiąga na krańcu przedziału : x⁴ + x² + 1 < 1 + 1 + 1 = 3 z drugiej strony x( x−1) ≤ 1/4 mnożąc stronami: − P(x) < 3/4, zatem P(x) > −3/4 i ostatecznie P(x) + 3/4 = W(x) > 0. Dobranoc! < t >

teofrast: Niestety, palnąłem głupstwo: o prawie trzeciej nad ranem nie panuję nad mózgiem. Napisałem i wykorzystałem bzdurę : x(x−1) ≤ 1/4 No to postaram się to naprawić... Myślę, że udało mi się znaleźć rozwiązanie, które miał na myśli pomysłodawca zadania... 1) z tw. Kartezjusza wynika, że dany w zadaniu wielomian W(X) nie ma pierwiastków ujemnych; 2) W(x) = x(1−x)(x⁴ + x² + 1) + 3/4 := P(x) + 3/4 przyjmuje wartości dodatnie dla x spoza (0, 1) 3) Pozostaje więc zbadanie istnienia pierwiastków wielomianu W(x) w przedziale ( 0, 1 ). W tym celu oszacujemy z dołu wartości P(x), korzystając z ogólnych własnosci wielomianów oraz geometrycznej interpretacji pochodnej w punkcie. a) P(x) ma tylko dwa rzeczywiste miejsca zerowe: 0 i 1. Wiadomo, że pomiędzy sąsiednimi miejscami zerowymi funkcja wielomianowa ma postać « garbu » ; P(x) przyjmuje w tym przedziale wartości ujemne i wierzchołek rzeczonego « garbu » jest zwrócony ku dołowi ( wypukłość w dół ) na garbie tym opiszmy trójkąt, którego podstawą jest przedział [0, 1], a ramionami styczne do wykresu wielomianu odpowiednio w punktach 0 oraz 1. b) równanie stycznej w punkcie 0: y − 0 = P'(0) ( x − 0 ) = −x c) równanie stycznej w punkcie 1`: y − 0 = P'(1) ( x − 1) = 3x − 3 ( gdzie P'(x) = 6x⁵ − 5x⁴ + 4x³ − 3x² + 2x − 1 ) d) szukamy współrzędnych wierzchołka trójkąta: 3x − 3 = −x ⇒ x = 3/4 oraz y = − 3/4. Zatem ekstremum « garbu » będzie miało wartość WIĘKSZĄ niż −3/4 e) konkludujemy przeto, iż P(x) > −3/4 ⇒ W(x) = P(x) + 3/4 > 0 na (0, 1) ⇒ w tym przedziale również nie ma pierwiastków. W(x) nie posiada zatem żadnych pierwiastków. Myślę, że rozwiązanie jest dość eleganckie, ale bardzo mi się spodobała propozycja ICSP sprowadzenia wielomianu do postaci quasi−kanonicznej...

teofrast: Mała errata do punktu 2) winno być: « P(x) + 3/4 przyjmuje wartości dodatnie dla DODATNICH x spoza (0, 1) »

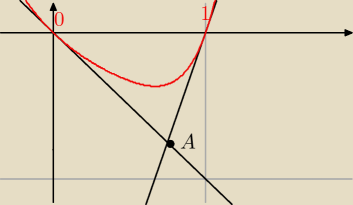
teofrast: A ( 3/4, −3/4 )

teofrast: Mała errata do puntu 2: oczywiście znów chochlik; winno być: 2) W(x) = x(x−1)(x⁴ + x² + 1) + 3/4 przyjmuje wartości dodatnie dla x spoza (0, 1)

teofrast: I w takim układzie punkt 1) ( tw. Kartezjusza ) można sobie darować...

Eta: Np. taki sposób: x⁷+1=0 −− jedynym rozwiązaniem rzeczywistym jest x= −1 x⁷+1= (x−1)(x⁶−x⁵+x⁴−x³+x²−x+1)

	3		x7+1		1
to: x6−x5+x4−x3+x2−x+		=		−
	4		x+1		4

	x7+1		1
x≠−1 ⇒		−		−−−− brak rozwiązań rzeczywistych
	x−1		4

Eta: W mianowniku oczywiście miało być x+1

PW:

	3		3
x6+x4+x2 − (x5+x3+x) +		= x2(x4+x2+1) − x (x4+x2+1) +		=
	4		4

	3
= (x4+x2+1) (x2−x)+		.
	4

Jak już pisaliście, nie ma problemu z x>1 i x≤0. Dla x z przedzialu 0,1 napisze dalej jak zresetuje, klawiatura zwariowala

Eta:

PW: Mamy iloczyn dwóch wielomianów: u(x) = x⁴+x²+1 i v(x) = x²−x Na przedziale (0,1) oczywiste są nierówności

	1
1<u(x)<3 i −		≤v(x)<0,
	4

z których wynika

	3
−		<u(x)v(x) <0,
	4

skąd

	3
u(x)v(x) +		>0
	4

teofrast: « z których wynika » ... Jak wynika?, bardzo mnie interesują szczegóły...Dziękuję z góry!

PW: Nie przesadzaj, to zwykłe mnożenie stronami przez liczbę dodatnią.

	1
−		≤v(x)
	4

mnożymy przez u(x)>0:

	u(x)
(1) −		≤u(x)v(x).
	4

Z nierówności 1<u(x)<3

	1
pomnożonej stronami przez (−		) wynika
	4

	−1		−u(x)		−3
(2)		>		>		.
	4		4		4

Zastosowanie "prawej" nieórności (2) do lewej strony (1) kończy dowód.

teofrast: Racja. gratuluję. wczoraj byłem bliski tego, ale jakoś mi się pokiełbasiło...To już mamy 4 sposoby na udowodnienie braku pierwiastków. No to ja jeszcze dorzucę kolejny: Po ustaleniu, że ewentualne pierwiastki moga być zlokalizowane jedynie w przedziale (0, 1), zapisujemy W(x) następująco: W(x) = x⁶ − x + 3/4 + (x⁴ − x⁵) + ( x² − x³ ).Wyrazenia w nawiasach są dodatnie dla x∊(0, 1). Dla x⁶ − x + 3/4 łatwo sprawdzić dodatnią okresloność na (0,1) dowolnym sposobem, np. wyznaczając najmniejszą wartość na (0,1)...

PW: No to już mamy niemal festiwal rozwiązań, a pablo nic, zadał pytanie i cieszy się, że nie śpimy po nocach. Dobranoc.

teofrast: Dobranoc. Społeczeństwo polskie jest postproletariackie...Czemu więc się dziwić...

asdf: ...dlaczego tak sądzisz bo nie siedzi po nocach i nie robi z matematyki? Nie kazdy ma taką potrzebe..