Twierdzenie sinusów i cosinusów
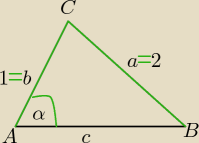
Hajtowy: W trójkącie ostrokątnym dane są: a = 2 cm, b = 1 cm, sinα =
2√23 (przez 3, bo nie
widać). Oblicz c.
Wiem, że było już takie zadanie :
https://matematykaszkolna.pl/forum/133881.html Ale nie jest rozwiązane

Proszę o rozwiązanie całego
poprzez Twierdzenie sinusów i cosinusów
Dziękuję


20 maj 15:53
Hajtowy: Help

20 maj 16:09
ICSP: wystarczy samo twierdzenie cosinusów.
Naprzeciwko którego boku jest kąt α ?
20 maj 16:21
Hajtowy: Naprzeciwko a czyli |BC|
No ale ja nie wiem jak zrobić

20 maj 16:24
ICSP:
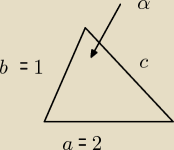
Z twierdzenia cosinusów :
a
2 = b
2 + c
2 − 2ab * cosα
wystarczy podstawić.
20 maj 16:29
ICSP: −2bccosα oczywiście
20 maj 16:29
Hajtowy: 4=1+c2−2c2cosα
3=c2−2c2cosα
cosα − ile tu jest?
cos30 czy ilu ?
20 maj 16:31
ICSP: masz podany sinα więc przelicz go na cosα
i Popraw równanie. Masz o jeden kwadrat za dużo.
20 maj 16:33
Hajtowy: 4=1+c
2−2c * cosα
3=c
2−2c*cosα
Jak mam sinα zamienić na cosα ?
Nie umiem

20 maj 16:34
20 maj 16:35
Hajtowy: cosα=
13 ?

20 maj 16:35
ICSP: | | 1 | |
tak cosx = |
| bo masz trójkąt ostrokątny |
| | 3 | |
20 maj 16:36
Hajtowy:
c
2−2c−9=0
Δ=4+36=40

20 maj 16:37
Mila:
| | 2√2 | |
sinα= |
| , cosα>0 ( bo kąt jest ostry) |
| | 3 | |
a
2=b
2+c
2−2*bccosα
3c
2−2c−9=0
Δ=4+4*9*3=4+108=112
√112=4
√7
| | 2−4√7 | | 2+4√7 | |
c= |
| <0 lub c= |
| |
| | 6 | | 6 | |
20 maj 16:38
ICSP: jeszcze raz
20 maj 16:38
Hajtowy: ehh... Mila dziękuję, ale chciałem też się sam pomęczyć

ICSP Tb też dzięki

20 maj 16:40
 Proszę o rozwiązanie całego
poprzez Twierdzenie sinusów i cosinusów
Dziękuję
Proszę o rozwiązanie całego
poprzez Twierdzenie sinusów i cosinusów
Dziękuję



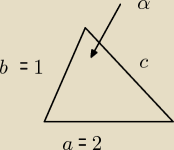 Z twierdzenia cosinusów :
a2 = b2 + c2 − 2ab * cosα
wystarczy podstawić.
Z twierdzenia cosinusów :
a2 = b2 + c2 − 2ab * cosα
wystarczy podstawić.




 ICSP Tb też dzięki
ICSP Tb też dzięki 