 Jakby ktoś mógł chociaż 1 rozwiązać, to już bd baardzo wdzięczna
Jakby ktoś mógł chociaż 1 rozwiązać, to już bd baardzo wdzięczna  1) Na hiperboli X2 − y2 = 4 wyznacz punkt leżący najbliżej punktu (0,2)
2) Znajdź wymiary walca o największej objętości i takiego, że jego całkowita powierzchnia
wynosi 6 π
3) Znajdź wymiary prostopadłościanu o największej objętości i podstawie kwadratowej, którego
przekątna ma długość 8√2
1) Na hiperboli X2 − y2 = 4 wyznacz punkt leżący najbliżej punktu (0,2)
2) Znajdź wymiary walca o największej objętości i takiego, że jego całkowita powierzchnia
wynosi 6 π
3) Znajdź wymiary prostopadłościanu o największej objętości i podstawie kwadratowej, którego
przekątna ma długość 8√2
| x2 | y2 | |||
4) W elipsę | + | = 1 wpisano prostokąt o największym polu. Oblicz to pole. | ||
| 16 | 4 |


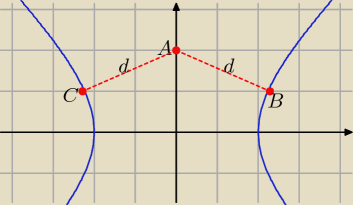 x2 − y2 = 4
y = √x2 − 4 (górne gałęzie hiperboli) lub y = −√x2 − 4 (dolne gałęzie).
Bierzemy y = √x2 − 4 i szukamy punktu B lub C leżących najbliżej punktu A(0, 2), przy czym
|AB| = |AC| = d, B = (x0, y0) = (x0, √x02 − 4)
d = √(x0 − 0)2 + (y0 − 2)2 → minimum,
Wstaw √x02 − 4 w miejsce y0, otrzymasz d(x0), wyznacz pochodną d'(x0)
i na jej podstawie wyznacz minimum funkcji d(x0),
Powinno wyjść: x0 = √5 i y0 = 1 lub x0 = −√5 i y0 = 1
x2 − y2 = 4
y = √x2 − 4 (górne gałęzie hiperboli) lub y = −√x2 − 4 (dolne gałęzie).
Bierzemy y = √x2 − 4 i szukamy punktu B lub C leżących najbliżej punktu A(0, 2), przy czym
|AB| = |AC| = d, B = (x0, y0) = (x0, √x02 − 4)
d = √(x0 − 0)2 + (y0 − 2)2 → minimum,
Wstaw √x02 − 4 w miejsce y0, otrzymasz d(x0), wyznacz pochodną d'(x0)
i na jej podstawie wyznacz minimum funkcji d(x0),
Powinno wyjść: x0 = √5 i y0 = 1 lub x0 = −√5 i y0 = 1
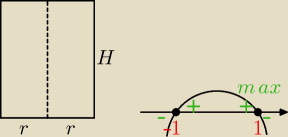 Zadanie 2.
Zadanie 2.
| 3 − r2 | ||
2πr2 + 2πrH = 6π ⇒ r2 + rH = 3 ⇒ H = | , r, H > 0 | |
| r |
 Jesteś genialny
Jesteś genialny  Analizuję zad 1 i kompletnie nie wiem jak obliczyć
d'(xo). Wychodzą mi takie rzeczy z kosmosu, które pierwszy raz na oczy widzę
Analizuję zad 1 i kompletnie nie wiem jak obliczyć
d'(xo). Wychodzą mi takie rzeczy z kosmosu, które pierwszy raz na oczy widzę Mógłbyś mi
wyjaśnić, jak to policzyć
Mógłbyś mi
wyjaśnić, jak to policzyć Za 2 się nawet jeszcze nie zabrałam
Za 2 się nawet jeszcze nie zabrałam Ale zaraz się zabiorę, może
to mi bd lepiej szło
Ale zaraz się zabiorę, może
to mi bd lepiej szło  W każdym razie dziękuję
W każdym razie dziękuję 
 Jakieś takie prostsze od tego 1
Jakieś takie prostsze od tego 1 
| 8√2 | ||
Czy w 3 powinny wyjść tak kosmiczne liczby, jak √ | (to wszystko jest pod | |
| 3 |
 A pozostałych nie umiem
dalej
A pozostałych nie umiem
dalej
 ************************************************
************************************************
 W każdym razie dziękuję
W każdym razie dziękuję 
| 8√2 − b2 | ||
stosować pierwiastków. Wyszło mi zatem : V(b) = | * b | |
| 2 |
| 1 | 1 | |||
Natomiast pochodne to: (podstawiając 1 x) − P'(y) = 16 * y * (4y2 − 16)− | (ta − | |||
| 2 | 2 |
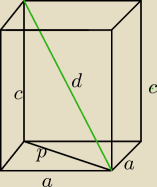 3)
d=8√2
d2=p2+c2
(8√2)2=a2+a2+c2
64*2=2a2+c2
c2=128−2a2
c=√128−2a2
V(a)=a2*√128−2a2
3)
d=8√2
d2=p2+c2
(8√2)2=a2+a2+c2
64*2=2a2+c2
c2=128−2a2
c=√128−2a2
V(a)=a2*√128−2a2
| −4a | 2a3 | |||
V'(a)=2a*√128−2a2+a2* | =2a√128−2a2− | ⇔ | ||
| 2√128−2a2 | a2*√128−2a2 |
| 2a(128−2a2)−2a3 | ||
V'(a)= | ||
| √128−2a2 |
| 256a−4a3−2a3 | ||
V'(a)= | ||
| a2*√128−2a2 |
| 8√6 | ||
a=c= | ||
| 3 |
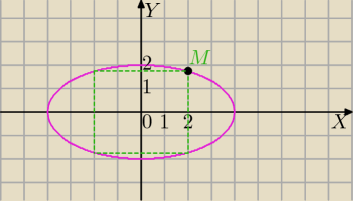 4)
4)
| x2 | y2 | ||
+ | =1 | ||
| 16 | 4 |
| y2 | x2 | ||
=1− | /*4 | ||
| 4 | 16 |
| x2 | ||
y2=4− | ||
| 4 |
| 16−x2 | ||
y2= | ||
| 4 |
| √16−x2 | ||
y= | ||
| 2 |
| √16−x2 | ||
M=(x, | ) | |
| 2 |
| √16−x2 | ||
P▭=4x*y=x* | ||
| 2 |
| −2x | ||
P'=2*√16−x2+2x* | ||
| 2√16−x2 |
 Np. w 3 kompletnie nie rozumiem 3 linijki. Tam, gdzie (8√2)2
jest podstawione do wzoru objętości. Ale nie chcę Cię już męczyć bardziej
Np. w 3 kompletnie nie rozumiem 3 linijki. Tam, gdzie (8√2)2
jest podstawione do wzoru objętości. Ale nie chcę Cię już męczyć bardziej 
 W
każdym razie nie rozumiem
W
każdym razie nie rozumiem
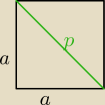 d2=p2+c2 z tw. Pitagorasa, masz braki z LO.
p − przekątna podstawy, czyli kwadratu o boku a
p2=a2+a2
p2=2a2
d2=p2+c2 z tw. Pitagorasa, masz braki z LO.
p − przekątna podstawy, czyli kwadratu o boku a
p2=a2+a2
p2=2a2
 Przepraszam za kłopot. Teraz znowu nie rozumiem pochodnej (też 3).
Przepraszam za kłopot. Teraz znowu nie rozumiem pochodnej (też 3).

 Smacznego
Smacznego  Jakby co to się odezwę
Jakby co to się odezwę 
 A w 4 wyszło mi x=2√2, y=√2, czyli P=16. Jest dobrze, że znowu
gdzieś błąd popełniłam?.
A w 4 wyszło mi x=2√2, y=√2, czyli P=16. Jest dobrze, że znowu
gdzieś błąd popełniłam?.
 Dziękuję Ci, naprawdę bardzo mi pomogłaś
Dziękuję Ci, naprawdę bardzo mi pomogłaś  1 i 5 sobie już chyba daruję, bo
nie mam sumienia i tym jeszcze Ci głowę zawracać, jak i tak masz mnie już pewnie dosyć
1 i 5 sobie już chyba daruję, bo
nie mam sumienia i tym jeszcze Ci głowę zawracać, jak i tak masz mnie już pewnie dosyć 
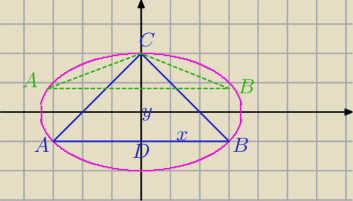 Postaraj się 5 rozwiązać, to przecież elipsa.
x2 + 3y2 = 12 /:12
Postaraj się 5 rozwiązać, to przecież elipsa.
x2 + 3y2 = 12 /:12
| x2 | y2 | ||
+ | y2=1 | ||
| 12 | 4 |
| x2 | y2 | ||
+ | =1 postac kanoniczna | ||
| (2√3)2 | 22 |
| 1 | ||
y2=4− | x2 | |
| 3 |
| 1 | ||
PΔ=2* | x*(2−√4−(1/3)x2)⇔P'(x)=0 dla x=0 nie odpowiada warunkom zadania | |
| 2 |
| 2√36−3x2−2x2+12 | ||
P'= | ||
| √36−3x2 |
| 1 | ||
Liczę pole Δ CDB Niebieskiego, | |CD|*|DB| | |
| 2 |
 CD i BD
CD i BD
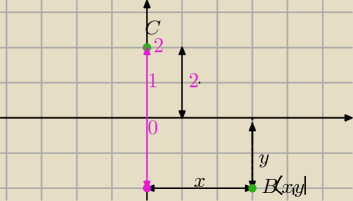 W Twoim zadaniu
x −wsp x−owa punktu B na elipsie ( właśnie ją chcemy policzyć)
y=−√4−(1/3)x2 dla obranej x
Ale wysokość liczymy h=CD=2+|−√4−(1/3)x2|=2+√4−(1/3)x2
W Twoim zadaniu
x −wsp x−owa punktu B na elipsie ( właśnie ją chcemy policzyć)
y=−√4−(1/3)x2 dla obranej x
Ale wysokość liczymy h=CD=2+|−√4−(1/3)x2|=2+√4−(1/3)x2
 Dziękuję pięknie
Dziękuję pięknie  Jesteś wielka
Jesteś wielka  Nigdy bym na to nie wpadła
Nigdy bym na to nie wpadła
 Jak tak patrzę teraz to wydaje się proste
Jak tak patrzę teraz to wydaje się proste 
