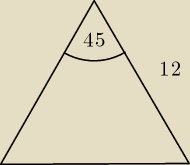
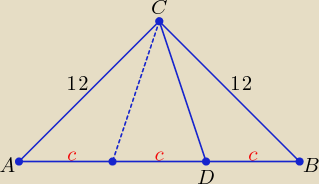
Trygonometria Licealista_Theosh: Siemka trygonomertia Ramię trójkąta równoramiennego ma długość 12 i tworzy z podstawą kąt o mierze 45⁰. a) Oblicz wysokość tego trójkąta poprowadzoną do podstawy. b) Z wierzchołka tego trójkąta poprowadzono odcinek dzielący kąt między ramionami w stosunku 2:1. Oblcz pole powstałych trójkątów. Chyba naryswałem dobry rysunek?

Mila: Zaznaczyłeś kąt 45⁰ między ramionami.

Mila: Dalej sam, czy rysować?

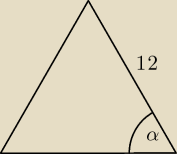
Licealista_Theosh: Fakt. Już poprawiam. α= 45⁰

Licealista_Theosh: Punkt a spoko zrobię:

	h
sin450=		⇒ 12sin450 =h
	12

gorzej z b.

Mila: a) 1) ΔACB jest równoramienny⇔∡A=∡B=45⁰⇒∡C=90⁰ 2)c²=12²+12² c=12√2 h=EB=6√2 b)

Mila:

	1
PΔABC=		*12*12=72
	2

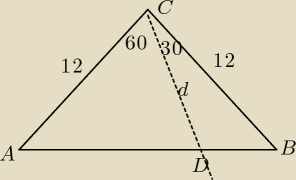
	1		√3
P1=		*12*d*sin60=6*d*		=3d*√3
	2		2

	1
P2=		*12*d*sin30=3d
	2

P₁+P₂=72 3d*√3+3d=72 3d(√3+1)=72 d(√3+1)=24/*(√3−1) d*(3−1)=24(√3−1) 2d=24(√3−1) d=12*(√3−1) podstaw do P₁ i P₂ P₁=3*12*(√3−1) *√3 P₂=3*12*(√3−1) sprawd rachunki, bo idę spac.

Licealista_Theosh: Dobranoc

Mila:

Eta:

Bogdan:

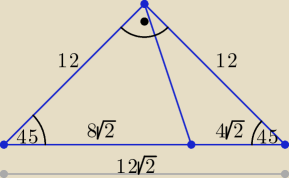
	1
Pole większego trójkąta: P1 =		*12*8√2*sin45o = 48
	2

	1
Pole mniejszego trójkąta: P2 =		*12*4√2*sin45o = 24
	2

Bogdan:

	1
Pole trójkąta ABC: P =		*12*12 = 72
	2

	2
Pole trójkąta ADC: P =		P = 48
	3

	1
Pole trójkąta DBC: P =		P = 24
	3

Mila: EB=6√2 h=6√2 tg75=2+√3

	h
tg75=
	ED

6√2
	=2+√3
ED

6√2=(2+√3)*|ED| /*(2−√3) 6√2*(2−√3)=(4−3)*|ED| 12√2−6√6=|ED| |DB|=6√2−12√2+6√6 |DB|=6√6−6√2≠4√2

Bogdan: Odcinek AB o długości 12√2 podzieliłem w stosunku 2:1 (w zadaniu podzielono nie odcinek AB, a kąt ACB), stąd moje |AD|=8√2 i |DB|=4√2 i z tymi wartościami obliczyłem pola trójkątów. Moje obliczenia są zgodne z przyjętymi oznaczeniami na moich rysunkach, ale oczywiście nie jest to zadanie przedstawione przez autora wątku. Błędnie odczytałem treść zadania, zacznę chyba okulary zakładać do czytania, pozdrawiam Milo

Mila: Napisałam sprostowanie, gdyż najczęściej uczniowie rozwiązują Twoim sposobem, to wielka pokusa podzielić tak podstawę przy podanej treści. Pozdrawiam

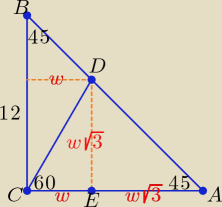
Bogdan: Proponuję takie rozwiązanie:

	1
|CA| = |CB| = 12, pole trójkąta ABC: P =		*12*12 = 72
	2

Trójkąt CED jest trójkątem o kątach 30^o, 60^o, 90^, stąd |DE| = w√3

	12
w + w√3 = 12 ⇒ w =
	√3 + 1

	1
Pole trójkąta CAD P1 =		*12*w
	2

Pole trójkąta CDB P₂ = P − P₁