Czworokąt opisany na okręgu Paweł: Na czworokącie ABCD opisano okrąg. Oblicz cos<BAD, wiedząc, że |AB| = 6, |BC| = 4, |CD| = 5, |AD| = 8.

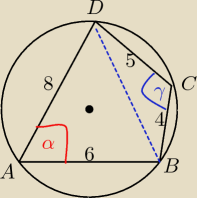
Mila: α+γ=180 cosα=−cosγ DB²=6²+8²−2*6*8*cosα=100−96cosα BD²=5²+4²−2*4*5cosγ=25+16+40cosα 100−96cosα=25+16+40cosα 136cosα=59

	59
cosα=
	136

Paweł: Z czego wynika, że cosα = −cosγ? Co się stało z DB²?

Mila: y=180−α cos(180−α) =−cosα wzory redukcyjne. DB² z dwóch Δ obliczyłam, są równe, w 5 linijce masz porównanie.

Paweł: Ok, wielkie dzięki za pomoc!

AS: W trójkącie ABC dane są: |AC|=2 pierwiastek z 7, |BC|= pierwisatek z 7 kąt BCA = 120 stopni. Oblicz długości odcinków, naj jakie dwisieczna kąta BCA dzieli bok AB.

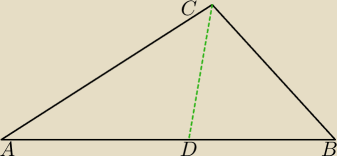
iteRacj@: Z twierdzenia cosinusów 543 oblicz długość boku AB. Na podstawie twierdzenia o dwusiecznej 498 oblicz długości AD i DB.