Promień okręgu wpisanego w trójkąt prostokątny jest równy 2. Tangens jednego z k szumi: Promień okręgu wpisanego w trójkąt prostokątny jest równy 2. Tangens jednego z kątów ostrych trójkąta wynosi 3/4. Oblicz odległość miedzy wierzchołkiem kąta prostego a punktem styczności okręgu z przeciwprostokątną.

bednarz: https://matematykaszkolna.pl/forum/194409.html

Klara:

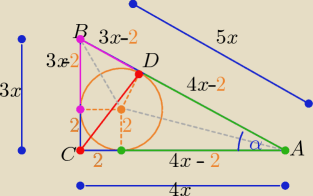
	3
tgα=		to |BC|= 3x, |AC|=4x , x>0 ⇒ |AB|=5x
	4

|AB|= 7x−4 ⇒ 7x−4=5x ⇒ x=2 to: |AB|= 10 , |BC|=6, |AC|=8 , |AD|= 6 , |BD|= 4

	8		4
cosα=		=
	10		5

z twierdzenia kosinusów w trójkącie CAD |CD|²= 8²+6²−2*8*6*cosα=.......... dokończ i otrzymasz:

	2√145
odp: |CD|=
	5