planimetria albina: Promień okręgu wpisanego w trójkąt prostokątny jest równy 2. Tangens jednego z kątów ostrych trójkąta wynosi ³₄. Oblicz odległość miedzy wierzchołkiem kąta prostego a punktem styczności okręgu z przeciwprostokątną. proszę o pomoc

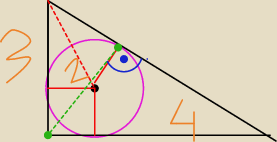
iiiii: liczysz z tw pitagorasa tą przerywaną linie czerwoną pozniej znow z tw pitagorasa liczysz ten krotszy odcinek na ktory dzieli przeciwprostokatna ten zielony punkt i na koncu liczysz zielona przerywana z tw pitagorasa

albina: dziękuję zrobiłem właśnie sama podobnym sposobem i też wyszło

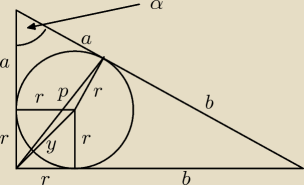
Kipic: A ja bym tak zrobił

	3
tgα=
	4

y=2√2 r=2 jedna z przyprostokatnych ma dlugosc krótsza 3x dłuższa 4x a=3x−2 b=4x−2 a+b=5x 3x−2+4x−2=5x 7x−4=5x 2x=4 x=2 a=3x−2 b=4x−2 a=4 b=6 i p z twierdzenia cosiunusów

wr: ∞≥βπΩ→βγδ

Pudzian: ∞≥βπΩ→βγδ