ef sinus: Dany jest trójkątt prostokatny ABC, w którym |<A| = 90. Przeciwprostokatna BC ma dlugość a , dwusieczna AD kąta prostego ma długość d. Udowodnij, ze pole trójkata ABC jest równe P =¹₄(d² + d√d² + 2a²)

sinus: ?

sinus: up

Mila: Wpiszę po kolacji.

sinus: okey

Eta:

	bc
P(ABC)=		⇒ 2bc= 4P
	2

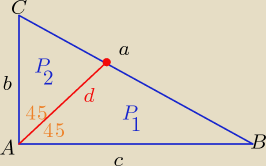
	db		dc		d
P(ABC)= P1+P2=		*sin45o+		*sin45o=		√2(b+c)
	2		2		4

	d√2
P=		(b+c) /2
	4

	d2		d2
P2=		(b2+c2+2bc) =		(a2+4P) /*8
	8		8

8*P²−4d²*P−d²a²=0 Δ=16d⁴+32d²a² , √Δ= 4d*√d²+2a²

	4d2+4d√d2+2a2		1
P=		=		[d2+d√d2+2a2]
	16		4

c.n.u

sinus: dziękuje

Mila: O, jak miło, Eta już wpisała.

sinus: a czy mogła byś mi pomoc z takim zadaniem https://matematykaszkolna.pl/forum/202059.html