| 1 | ||
niektórych kątów. Jest tam m.in. cos60°= | . Byłoby dobrze, tylko tam minus.. No to | |
| 2 |
| 1 | ||
cos120°=− | . | |
| 2 |
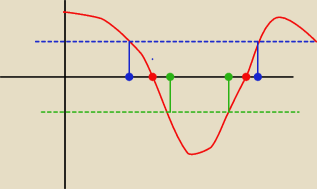 z rusunku widzimy, że cos dla kąta 60 stopni (co jest w tablicach maturalny ) wynosi 0.5
Z koleji caly wykres funkcji cos jest symetryczny co za tym idzie jezeli niebieska kropka to
kąt 60 stopni a czerwona to 90 stopni to w takim razie od kropki niebieskiej do czerwonej jest
30 stopni, dodatkowo widzimy ze odleglosc kropki czerwonej od zielonej jest taka sama jak
kropki niebieskiej do zielonej czyli 30 stopni zatem pierwsza z koleji kropka zielona jest w
punkcie 120 stopni < wtedy to cos120=−0.5
analogicznie widac ze druga kropka czerwona jest w punkcie 270 stopni czyli zielona jest w
punkcie 270−30=240 stopni ( wtedy tez cos240=−0.5)
Jednak zapisuje sie to zazwyczaj w radianach i bardziej ogolnie mianowicie w taki sposob :
cosx=−0.5 ⇔ x=2pi/3 +2kpi gdzie k nalezy do calkowitych ( 2pi/3 to 120 stopni funkcja jedst
okresowa zatem wartosc −0,5 powtarza sie co 2pi )
lub x=7pi/6 +2kpi ( 7pi/6=240 stopni )
z rusunku widzimy, że cos dla kąta 60 stopni (co jest w tablicach maturalny ) wynosi 0.5
Z koleji caly wykres funkcji cos jest symetryczny co za tym idzie jezeli niebieska kropka to
kąt 60 stopni a czerwona to 90 stopni to w takim razie od kropki niebieskiej do czerwonej jest
30 stopni, dodatkowo widzimy ze odleglosc kropki czerwonej od zielonej jest taka sama jak
kropki niebieskiej do zielonej czyli 30 stopni zatem pierwsza z koleji kropka zielona jest w
punkcie 120 stopni < wtedy to cos120=−0.5
analogicznie widac ze druga kropka czerwona jest w punkcie 270 stopni czyli zielona jest w
punkcie 270−30=240 stopni ( wtedy tez cos240=−0.5)
Jednak zapisuje sie to zazwyczaj w radianach i bardziej ogolnie mianowicie w taki sposob :
cosx=−0.5 ⇔ x=2pi/3 +2kpi gdzie k nalezy do calkowitych ( 2pi/3 to 120 stopni funkcja jedst
okresowa zatem wartosc −0,5 powtarza sie co 2pi )
lub x=7pi/6 +2kpi ( 7pi/6=240 stopni )
