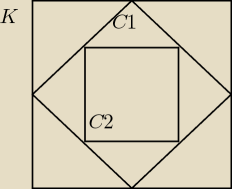
 Pole kwadratu K jest równe 8. Środki boków tego kwadratu połączono, tworząc czworokąt C1.
Następnie połączono środki boków czworokąta C1, tworząc czworokąt C2. W podobny sposób
utworzono czworokąty C3, C4...
Suma pól czworokątów K+C1+C2+...+Cn jest równa 1534 .
Znajdź liczbę n.
Otóż mam problem, ponieważ wiem, że wynik powinien być równy 5. Stworzyłam ciąg, gdzie
a1=poleC1 , a2=poleC2, a q=12 , więc a1=4; a2=2
Sn=1534=634 ; 634=4*1−qn1−q , z tego działania wyszło mi potem coś
takiego:
3132= −(12)n i nie wiem co z tym dalej zrobić...
wiem, że pole pierwszego kwadratu nie wlicza się do ciągu, ale kiedy obliczyłam to zadanie w
ten sam sposób, jednak uwzględniając pole kwadratu "K" to wyszedł mi ładny wynik, mianowicie
6, potem tylko odjęłam 1, więc w sumie n=5, ale zastanawiam się co robię źle w moim pierwszym
sposobie, gdzie w ciągu pól tych kwadratów nie uwzględniłam pola kwadratu K.
Bardzo proszę o pomoc
Pole kwadratu K jest równe 8. Środki boków tego kwadratu połączono, tworząc czworokąt C1.
Następnie połączono środki boków czworokąta C1, tworząc czworokąt C2. W podobny sposób
utworzono czworokąty C3, C4...
Suma pól czworokątów K+C1+C2+...+Cn jest równa 1534 .
Znajdź liczbę n.
Otóż mam problem, ponieważ wiem, że wynik powinien być równy 5. Stworzyłam ciąg, gdzie
a1=poleC1 , a2=poleC2, a q=12 , więc a1=4; a2=2
Sn=1534=634 ; 634=4*1−qn1−q , z tego działania wyszło mi potem coś
takiego:
3132= −(12)n i nie wiem co z tym dalej zrobić...
wiem, że pole pierwszego kwadratu nie wlicza się do ciągu, ale kiedy obliczyłam to zadanie w
ten sam sposób, jednak uwzględniając pole kwadratu "K" to wyszedł mi ładny wynik, mianowicie
6, potem tylko odjęłam 1, więc w sumie n=5, ale zastanawiam się co robię źle w moim pierwszym
sposobie, gdzie w ciągu pól tych kwadratów nie uwzględniłam pola kwadratu K.
Bardzo proszę o pomoc
| 1−qn | ||
Sn= a1 * | ||
| 1−q |
| 3 |
| ||||||||||||
15 | =8* | ||||||||||||
| 4 |
|
| 63 |
| |||||||||||
= | ||||||||||||
| 4 |
|
| 63 | 1 | ||
=16*(1−( | )n) | ||
| 4 | 2 |
| 63 | 1 | ||
=16−16( | )n | ||
| 4 | 2 |
| 1 | ||
63=64−64( | )n | |
| 2 |
| 1 | ||
−1=−64( | )n /: (−64) | |
| 2 |
| 1 | 1 | ||
=( | )n | ||
| 64 | 2 |
| 1 | 1 | |||
( | )6=( | )n | ||
| 2 | 2 |
 Podobne zadanko dzis wykonywalem :
http://forum.zadania.info/viewtopic.php?f=31&t=6549 , mozna porownac sposob zapisow
Podobne zadanko dzis wykonywalem :
http://forum.zadania.info/viewtopic.php?f=31&t=6549 , mozna porownac sposob zapisow 
| 3 | ||
"Suma pól czworokątów K+C1+C2+...+Cn jest równa 15 | ." | |
| 4 |