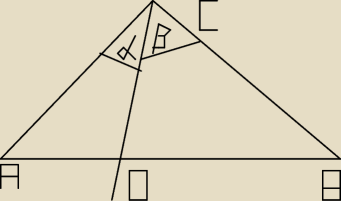
Zadanie na wykaż. Kinia: Punkt D należy do podstawy AB trójkąta równoramiennego ABC. Półprosta CD^→ dzieli kąt przy wierzchołku C na kąty o miarach α i βwykaż, że ^IADI_IDBI = ^sinα_sinβ.

Eta: https://matematykaszkolna.pl/forum/201179.html

Kinia: Z założeniami zawsze idzie mi najtrudniej i nigdy nie wiem od czego zacząć... Mam korzystać z twierdzeń? Czy najzwyklejszych wzorów? Mogę poprosić o wskazówki?

Kinia: Mógłby ktoś dopomóc...?

Kinia: Mógłby ktoś powiedzieć od czego zacząć...? z czego skorzystać...?

Eta:

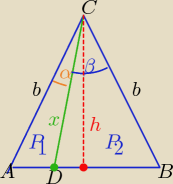
	1		1		P1		|AD|
P1=		|AD|*h , P2=		|DB|*h ⇒		=
	2		2		P2		|DB|

	1		1		P1		sinα
P1=		*b*x*sinα , P2=		*b*x*sinβ ⇒		=
	2		2		P2		sinβ

	|AD|		sinα
zatem mamy tezę:		=
	|DB|		sinβ

c.n.u

Eta:

Kinia: Dziękuję bardzo... Analizuję każde po kolei zadanie... Dlatego tak "od razu" nie odpisuję... Ale dziękuję i jestem bardzo wdzięczna za pomoc − zawsze

Eta:

Krzysiek : Eta jesli sa zadania z geometrii to na Ciebie zawsze mozna liczyc l

Eta: