Przeciwprostokątna. Kinia: W trójkącie prostokątnym ABC, w którym kąt ∡C = 90^o i BC < AC, poprowadzono prostą przez wierzchołek C trójkąta, która przecina przeciwprostokątną w punkcie D takim, że AD : DB = 2:1. Wiedząc, że BC= √3 cm i ∡DCB = 30^o oblicz |AB|.

Eta: @Kinia .......... może popracuj trochę sama? co? Napisz jak rozwiązujesz, sprawdzimy ..... bo matura ..tuż, tuż

Kinia: Jam pierwsza klasa Spróbuję... Ale proszę o sprawdzenie... nakierowanie... Nie chcę mieć rozwiązanego − choć ułatwia to sprawę. Ale rady by się przydały... Z czego skorzystać najlepiej itp. =)

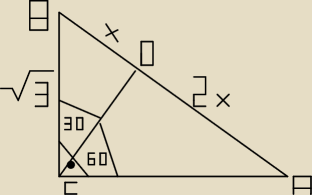
Kinia: Czy kąt BDC to 90^o? Czy kąt ADC to również 90^o? Potem pitagoras?

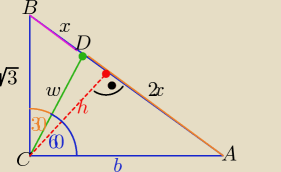
Eta: |∡ADC| ≠ 90^o

	1		1		P(ADC)
P(ADC)=		*2x*h , P(CDB)=		*x*h ⇒		= 2
	2		2		P(CDB)

	1		bw√3
oraz: P(ADC=		*b*w*sin60o=
	2		4

	1		w√3
P(CDB)=		*w*√3*sin30o=
	2		4

	P(ADC)		bw√3
zatem		=		= b ⇒ b=2
	P(CDB)		w√3

i teraz z tw. Pitagorasa |AB|²=........... dokończ odp: |AB|= √7

Kinia: Dziękuję ślicznie za pomoc =)