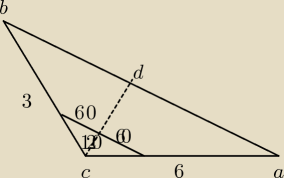
Związek promieni i długość odcinka. Kinia: W trójkącie ABC dane są kąt ∘ |∡ACB | = 120^o , |AC | = 6 i |BC | = 3 . Dwusieczna kąta ∡ACB przecina bok AB w punkcie D . a) Oblicz długość odcinka CD . b) Jaki jest związek miedzy długościami promieni: okręgu opisanego na trójkącie ADC i okręgu opisanego na trójkącie DBC ? Odpowiedź uzasadnij.

Eta: https://matematykaszkolna.pl/forum/201179.html

Kinia: Mogłabym liczyć na jakieś rady...?

bysztszak:

3		6
	=
|BD|		|DA|

|BD|=x |DA|=2x cos120=−sin30

bysztszak: czekaj, źle nie o to pytają

Eta:

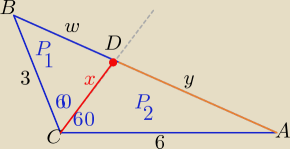
	3		6
Z twierdzenia o dwusiecznej:		=		⇒ y= 2w
	w		y

P(ABC)= P₁+P₂

	1
P(ABC)=		*3*6*sin120o= 9*sin60o ( sin120o= sin60o
	2

	1		1
P1=		*3*x*sin60o , P2=		*6*x*sin60o
	2		2

	9
9*sin60o=		*x*sin60o ⇒ x=2
	2

b) w trójkątach CDB i ACD

	w		y		2w
R1=		i R2=		=
	2sin60o		2sin60o		2sin60o

	R2
to		= 2 ⇒ R2=2*R1
	R1

Kinia: Tutaj również Ci dziękuję