Zadanie na "wykaż". Kinia: W trójkącie prostokątnym ABC, w którym ∡C = 90^o, poprowadzono odcinek CD w taki sposób, że D ∊\in AB oraz ∡BCD = 2 ∡ACD. Wykaż, że jeżeli pole trójkątów ADC i BCD są równe, to kąty ostre trójkąta ABC mają miarę 30^o i 60^o.

Eta: https://matematykaszkolna.pl/forum/201179.html

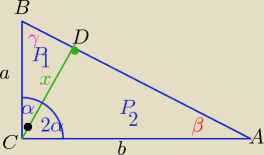
Eta: Z założenia: 3α=90^o ⇒ α=30^o i 2α=60^o P₁=P₂

	1		xa		1		x*b√3
P1=		*x*a*sin30o =		, P2=		*x*b*sin60o=
	2		4		2		4

to: a= b√3

	a		b√3
tgβ=		=		= √3 ⇒ β = 60o , to γ=.....
	b		b

Eta:

Kinia: Dziękuję