Obliczanie odcinka w trójkącie prostokątnym
Kinia: Na przedłużeniu przeciwprostokątnej AB trójkąta prostokątnego ABC obrano punkt D tak, ze BD=BC.
oblicz CD, jeśli wiadomo, ze BC=15cm i AC=8cm.
27 kwi 19:02
27 kwi 19:46
Kinia:
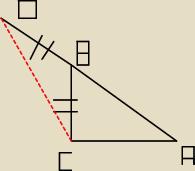
|BD|=|BC|=15cm
|AC|=8cm
Mam obliczyć pitagorasem |BA|?
Potem obliczyć na podstawie podobieństwa trójkątów?
27 kwi 20:00
Kinia: Mógłby ktoś doradzić...?
27 kwi 20:30
bysztszak: Twierdzeniem cosinusów spróbuj
27 kwi 21:15
Kinia:
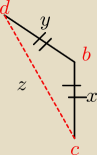
Przy b jest β
Przy d jest α
Przy c jest γ
Więc...
y
2=x
2+z
2−2xz*cosγ
z
2=x
2+y
2−2xy*cosβ
x
2=y
2+z
2−2yz*cosα
y i x jest równy 15cm
Co dalej...?
27 kwi 21:27
Eta:
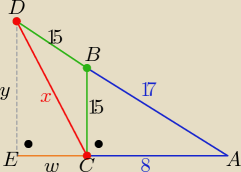
Jeden ze sposobów:
1/ z tw. Pitagorasa ... |AB|= 17
| | w | | 8 | | 8*15 | |
2/ z tw. Talesa |
| = |
| ⇒ w= |
| |
| | 15 | | 17 | | 17 | |
| | y | | 32 | | 15*32 | |
oraz |
| = |
| ⇒ y= |
| |
| | 15 | | 17 | | 17 | |
| | 120√17 | |
3/ z tw. Pitagorasa x2= y2+w2 =........ ⇒ x= |
| |
| | 17 | |
27 kwi 22:45
Kinia: Mogę spytać skąd to:
w15=817?
i to
y15=3217?
Nie znam tego z twierdzenia...
Znam tylko takie zależności:
8w=1715
88+w=1717+15
8+ww=17+1515
i z podobieństwa trójkątów bardziej niż z Talesa:
1717+15=17+1517+15+y
28 kwi 12:31
Eta:
@
Kinia ...doucz się nieco

| | 8 | | 17 | | w | | 8 | |
przecież : |
| = |
| ⇒ |
| = |
| |
| | w | | 15 | | 15 | | 17 | |
28 kwi 12:36
Eta:
Na przyszłość,to napisz przynajmniej z grzeczności słowo
dziękuję ... znasz takie?

28 kwi 12:51
Kinia: Tak, tak − piszę zawsze dziękuję...
Odpisałam Ci już niejednokrotnie w innych zadaniach, których mi pomogłaś =)
Dziękuję więc i teraz bardzo, ale to bardzo serdecznie

28 kwi 12:58
 |BD|=|BC|=15cm
|AC|=8cm
Mam obliczyć pitagorasem |BA|?
Potem obliczyć na podstawie podobieństwa trójkątów?
|BD|=|BC|=15cm
|AC|=8cm
Mam obliczyć pitagorasem |BA|?
Potem obliczyć na podstawie podobieństwa trójkątów?
 Przy b jest β
Przy d jest α
Przy c jest γ
Więc...
y2=x2+z2−2xz*cosγ
z2=x2+y2−2xy*cosβ
x2=y2+z2−2yz*cosα
y i x jest równy 15cm
Co dalej...?
Przy b jest β
Przy d jest α
Przy c jest γ
Więc...
y2=x2+z2−2xz*cosγ
z2=x2+y2−2xy*cosβ
x2=y2+z2−2yz*cosα
y i x jest równy 15cm
Co dalej...?
 Jeden ze sposobów:
1/ z tw. Pitagorasa ... |AB|= 17
Jeden ze sposobów:
1/ z tw. Pitagorasa ... |AB|= 17


