Sinusy w trójkącie Kinia: Dwa boki trójkąta mają długość a= 7 cm i b = 8 cm, a długość promienia okręgu wpisanego w ten trójkąt jest równa √5 cm. Wiedząc, ze pole trójkąta jest równe 12√5 cm², oblicz sinusy kątów tego trójkąta.

Eta: p −−− połowa obwodu, P−− pole trójkąta , r −− dł. promienia okręgu wpisanego R−− dł. promienia okręgu opisanego

	r
p=		2p=a+b+c ⇒ c= 2p−(a+b)
	P

	abc
R=
	4P

	a		b		c
sinα=		, sinβ=		, sinγ=
	2R		2R		2R

i działaj

Kinia: Można by prosić o pomoc w inny sposób − nie wykorzystując wzoru p=^r_P? Takowego nie poznałam, a póki nie jestem w 3 klasie nie mogę korzystać "czego chcę", choć byłoby tak prościej...

Eta: A taki poznałaś? P=r*p ( nie wierzę.........że nie ?

	r
z niego po przekształceniu : p=
	P

Kinia: Sprawdziłam ten wzór... Ogólnie to "p" oznacza połowę obwodu chyba... Jeśli tak − to nie poznałam...

Kinia: Mógłby ktoś doradzić...?

Kinia: Mogę liczyć na pomoc...? Jakiś zamiennik tego wzoru do tego zadania...?

Kinia: Mógłby ktoś doradzić z czego skorzystać...?

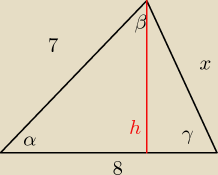
Saizou : P=12√5

	8*h
P=		=4h
	2

4h=12√5 h=3√5

	3√5
sinα=
	7

sin²α+cos²α=1

45
	+cosα=1
49

	4
cos2α=
	49

	2		2
cosα=		lub cosα=−
	7		7

z tw. cosinusów

	2
−dla cosα=
	7

	2
x2=72+82−2*7*8*
	7

x²=49+64−32 x²=81 x=9 x>0

	h		3√5		√5
sinγ=		=		=
	x		9		9

	1
12√5=		*7*9*sinβ
	2

	24√5		8√3
sinβ=		=
	63		21

	2
i analogicznie dla cosα=−
	7

Kinia: Dziaa!

Saizou : proszę, ale rachunków jest jeszcze trochę

Kinia: Wyniki w książce niby są: sinα=^√5₃ sinβ=^8√5₂₁ sinγ=^3√5₇ Ale spróbuję rozwiązać jeszcze raz jak Ty, sugerując się Twoimi krokami... Być może w książce się pomylili. Ale bardzo dziękuję =)

Saizou :

	√5
i chochlik jest u mnie przy sinγ=
	3

Kinia: @Saizou Mógłbyś znaleźć to "r" w drugim przypadku...? Ale pomóc znaleźć bok c...? https://matematykaszkolna.pl/forum/201066.html Tyle obliczeń, że nie sposób się nie pomylić − dziękuję za poświęcenie czasu i siły xD

Eta: Poprawiam swój zapis z (chochlikiem)

	P		12√5
p=		⇒ p=		= 12 , to 2p=24
	r		√5

c= 2p−(a+b) = 24−15= 9

	abc		7*8*9
R=		=		=.........
	4P		4*12√5

	a
sinα=		=..........
	2R

	b
sinβ=		=........
	2R

	c
sinγ=		=.........
	2R

dokończ....... to o wiele prostszy sposób rozwiązania tego zadania

Kinia: Nie mogę w ten sposób zrobić... Nie miałam wzoru z "p" jako połowa obwodu... Nauczyciel z matematyki nie toleruje "wyprzedzania" materiału, bo chce mieć pewność, że umiemy rozwiązywać zadania wszelkimi sposobami...

Kinia: Spróbowałam obliczyć Eta Twoim sposobem tylko sinα I wyszło mi R=⁵⁰⁴_48√5 R=^504√5₂₄₀ sinα=^a_2R= 7*²⁴⁰_504√5=^7*120*√5_252*5

Kinia: Ma wyjść sinα=^√5₃