Obliczanie pola trójkąta i promienia okręgu. Kinia: Na trójkącie ABC, w którym odcinek AC jest równy odcinkowi BC, opisano okrąg o środku O i promieniu R = 20 cm. Wiedząc, że ∠ AOB = 120^o, oblicz pole trójkąta ABC oraz promień okręgu wpisanego w ten trójkąt. Rozważ dwa przypadki. Mam na razie: Trójkąt ABC1 i on jest równoboczny, jego wysokość to 30 czyli bok 20 √3 czyli pole 300√3 Trójkąt ABC2 i on jest równoramienny jego pole jest trzecią częścią ABC1 czyli wynosi 100√3 Jak obliczyć wysokości, bo mam z tym problem...?

Kinia: Znaczy nie wysokość tylko promień okręgów.

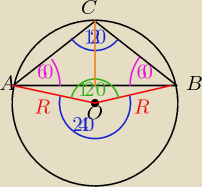
Saizou : I przypadek AB=a AC=BC=b i np. z tw. sinusów

a
	=2R
sin120

	√3
a=2R*sin120 sin120=sin(90+30)=cos30=
	2

	√3
a=2*20*
	2

a=20√3

	1   a 2
cos60=
	b

1		10√3
	=
2		b

b=20√3

	1
P=		*a*b*sinα
	2

	1		√3
P=		*20√3*20√3*
	2		2

P=10√3*10√3*√3=300√3

Saizou : a jeszcze promień okręgu wpisanego to

	2P
r=
	a+b+b

	600√3
r=
	3*20√3

	600√3
r=		=10
	60√3

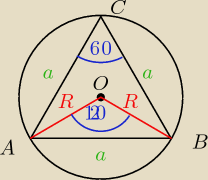
Saizou : II wersja

a
	=2*20
sin60

	√3
a=2*20*
	2

a=20√3

	(20√3)2√3
P=
	4

	1200*√3
P=		=300√3
	4

	2P
r=
	3a

	600√3
r=		=10
	3*20√3

Saizou : jeśli czegoś nie "spaprałem"

Kinia: Pierwszy przypadek ślicznie Drugi natomiast w odpowiedzi jest (spojrzałam dobrze xD) r = (20√3 cm²−30)cm

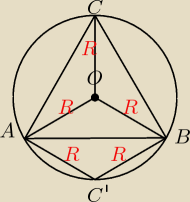
Saizou : teraz będzie II przypadek 3P_ABC'=P_ABC

	1
PABC'=		*300√3=100√3
	3

Kinia: Aaa, to są dwa sposoby, cudownie, ohoohohho Nio a jak mamy ten drugi przypadek go promień ile wyniesie?

Kinia: Mógłbyś ktoś wspomóc i pomóc obliczyć promień okręgu w trójkącie w drugim przypadku...? Wynik powinien wyjść: r = (20√3 cm2−30)cm

Kinia: Tutaj też mam problem, próbowałam rozwiązywać zasadą 30,60,90 stopni, potem pitagoras, ale nie wychodzi taki wynik... Ma ktoś pomysł, radę...?

Kinia: Hm...?

Kinia: Pomógłbyś ktoś, bo potrzebuję a nie ma naprawdę jak znaleźć odpowiedź... Proszę...

Kinia: To jak mamy ten trójkąt: −>https://matematykaszkolna.pl/forum/rysunek77521.png Mam użyć wzoru: r=^2P_a+b+c? r mam obliczyć... 2P = 420 a=R=15 b=R=15 c=...? Nie wiem ile wynosi bok c, wiadomo że ten trójkąt to nie równoboczny... Czyli c to nie 15...

Kinia: Pomógłby ktoś...?

Saizou : zauważ że kąt ∠AC'B=120^o

Kinia: Nie za bardzo wiem co dalej... Zrobiłabym to pitagorasem... Ale mam dwie nie wiadome... Nie znam boku c... Gdy wezmę pod uwagę 120 To będzie 30.60.90 Ale wtedy wychodzi, że to trójkąt równoboczny...

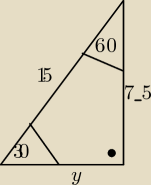
Kinia: y= ^√3₂*7,5 y=^15√3₄ r=^200√3_30+^15p{32

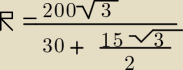
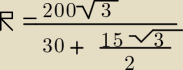Kinia: Bo nie widać tego zapisu tam... I ogólnie chodzi o to, że nie wychodzi...