g gg: Wyznacz wszystkie wartości a, dla których istnieje trójkąt o bokach długości 2, a+1 i 2a

Ajtek: Rozwiąż: 2+a+1>2a 2+2a>a+1 a+1+2a>2 Część wspólna będzie rozwiązaniem.

Edyta: muszą być spełnione wszystkie trzy warunki 2+a+1>2a 2+2a>a+1 a+1+2a>2

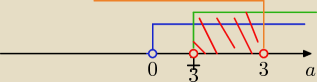
Eta: Aby istniał trójkąt o bokach a, b,c to: a,b,c >0 a+b>c i a+c>b i b+c>a 2+a+1>2a ⇒ a<3 i 2+2a>a+1 ⇒ a>−1 ⇒a >0

	1
i 2a+a+1>2 ⇒ 3a>1 ⇒ a>
	3

	1
zatem a € (		, 3)
	3

PW: A kto napisze, jaka jest teoretyczna podstawa tego "muszą być spełnione trzy nierówności"? Rozwiązując zadanie (zwłaszcza na egzaminie) powinniśmy napisać, z czego korzystamy − jest to twierdzenie, definicja, czy pewnik?

Eta: PeWnie ..........PW napisze

PW: za dowcip.A nie napiszę, niech młodzi sprawdzą w podręcznikach.

Edyta: z nierówności trójkąta https://matematykaszkolna.pl/strona/493.html

PW: Edyto, strona internetowa to nie podręcznik, tak się składa, że Autor nie napisał, co to jest − jest tam pewne stwierdzenie, prawie wszyscy to wiedzą. C o w i e d z ą? Tezę twierdzenia, czy treść pewnika?