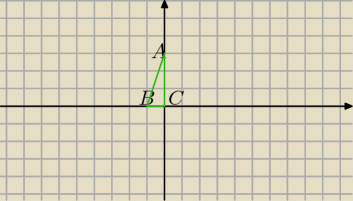
ZAdanie aaa: Wiadomo , że A=(0;3) B=(−1;0) C=(0;0). Znajdź równanie prostej w której zawiera się wysokość trójkąta ABC poprowadzona z wierzchołka C. Wysokosc trojkata to odcinek AC. Wiec ze wzoru na równanie prostej wyliczam szukana prostą: (y−3)(0−0)−(0−3)(x−0)=0 −(−3x)=0 3x=0 x=0 CZy wykonuje poprawnie te zdanie ? Moze gdzies robie błąd? Proszę o pomoc

politechniczny : a wysokość nie będzie czasami tak : prosta poprowadzona z wierzchołka C do połowy boku AB wtedy musisz policzyć połowę odcinak AB ze wzoru i potem napisać równanie prostej przechodzącej przez 2 punkty tak mi się wydaję

aaa: Potrzebuje konkretow

bezendu: tu coś podobnego masz https://matematykaszkolna.pl/strona/3224.html

aaa: no dobra rozmiem zadanie z podanego linku ale jak ono sie ma do mojego zadania. W moim przeciez trzeba znalesc rownanie prostej odcinka CA − przynajmniej ja to tak rozumiem, przeciez widac ze to trojkat a CA to jego wysokosc.. tylko ze mi nie wychodzi

politechniczny: skoro tak twierdzisz to napisz równanie prostej przechodzącej przez punkt B i C to chyba potrafisz

aaa: B=(−1,0) C=(0,0) (y−0)(0+1)−(0−0)(x+1)=0 y=0

aaa: i co dalej?

politechniczny : i sprawdź czy w książce jest taka odpowiedź

aaa: nie mam ksiazki robie te zadania z kartek ktore dostalem od korepetytora

politechniczny : no to masz już wyznaczoną tą prostą więc w czym problem

aaa: tu zadanie ktos wykonal tylko ja kompletnie nie rozumiem tego zapisu : https://matematykaszkolna.pl/forum/132873.html

politechniczny : gustlik wszystko ładnie rozpisał przecież

aaa: dobra jutro na korepetycjach to rozkminie, dzieki za pomoc

Basia: ⇒politechniczny spojrzałam, ale nie wiem o co Ci chodzi, bo podpowiedziałeś dobrze równanie prostej AB i prostopadłej do niej prostej CD albo wsp.AB^→ = [−1;−3] czyli pr.CD ma równanie −x − 3y + C = 0 0 − 0 + C = 0 −x − 3y = 0 x + 3y = 0 albo jak wolisz y = −¹₃x

politechniczny : czyli miałem racje wysokość trzeba było tak policzyć a nie tak jak to zrobił aaa

Basia: oczywiście; przecież tam jest wyraźnie napisane "Znajdź równanie prostej w której zawiera się wysokość trójkąta ABC poprowadzona z wierzchołka C."