| 2√2 | ||
W trójkącie ABC mamy dane: |AC| = 6 cm, |BC| = 4 cm oraz sin |∡ACB| = | . Oblicz obwód | |
| 3 |
| 4√2 | ||
Doszedłem do tego, że |AB| = | . | |
| sinβ |
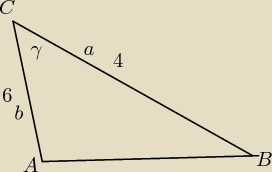 wyliczasz bok AB=c z tw cosinusów
c2=a2+b2−2abcosγ
wyliczasz bok AB=c z tw cosinusów
c2=a2+b2−2abcosγ
| AB | ||
i wtedy z tw sinusów masz | =2R | |
| sinγ |
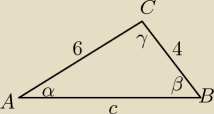 R− promien okręgu opisanego na Δ
R− promien okręgu opisanego na Δ
| 2√2 | ||
sinγ= | ||
| 3 |
| c | |
=2R, | |
| sinγ |
| 2√2 | ||
cos2α=1−( | )2 | |
| 3 |
| 8 | 1 | |||
cos2α=1− | ⇔cos2= | |||
| 9 | 9 |
| 1 | ||
cosα= | − Δostrokątny | |
| 3 |
| 1 | ||
cosα=− | − Δ rozwartokątny | |
| 3 |
| 1 | ||
c2=16+36−8*6* | ||
| 3 |
| 6 | 2√2 | 3 | |||
=2R, ⇔6:( | )=2R⇔6* | =2R | |||
| sinγ | 3 | 2√2 |
| 9 | |
=2R | |
| √2 |
| 9√2 | ||
R= | ||
| 4 |
| 1 | ||
II dla cosα=cosα=− | − Δ rozwartokątny | |
| 3 |
