funkcja kwadratowa, najmniejsza i największa wartość w przedziałach kldszt: Oblicz wartość najmniejszą i największą funkcji kwadratowej: f(x)= x² − 6x + 5 w każdym z przedziałów: a) <2,5> b)<5,6>

Tomek: https://matematykaszkolna.pl/strona/1683.html poczytaj trochę to nie jest wcale takie trudne....

kldszt: czyli po prostu np. w przykładzie a) podstawiam pod x 2, potem 3, potem 4, potem 5 i patrze która jest największa, a która najmniejsza?

kldszt: czy ten przedział to przedział rozwiązań?

Tomek: widze ze chyba nie skumałeś... to ci wytłumacze: liczysz wierzchołek: W=(p, q)

	−b
p=		=3
	2a

	−Δ
q=		=−4
	4a

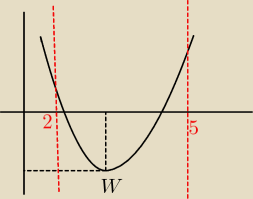
W=(3, −4) sprawdzasz czy wierzchołek należy do danego przedziału: przedział z podpkt a: widac ze należy bo p∊<2, 5> popatrz na równanie kwadratowe: ramiona skierowane do góry a wiec najmnejszą wartosc przyjmuje w wierzchołku (rysunek schematyczny to nie ma co na nim polegac teraz jak widac największa wartosc przyjmuje dla 2 lub 5 liczysz f(2) i f(5) która wartosc jest wieksza to jest właśnie wartosc najwieksza.. kumasz troche inaczej bd w b bo W nie należy do przedziału

kldszt: aaaa rozumiem wielkie dzięki geniusz a w b najmniejsza bedzie po prostu 5 a najwieksza 6?

Tomek: no musisz przeliczyc i która bedzie wieksza a która mniejsza... ciesze sie ze pomogłem