funkcja logarytmiczna marek: Do wykresu funkcji f(x)=a^x należny punkt (log₂3,9) a) Oblicz a 9=a^log₂3 3²=a^log₂3 log₂3=2 log₂3=2² czy ja dobrze robię? jak sie za to zabrać ? jak sie za to zabrać ?

irena_1: a^log₂3=9 log₂3*log₂a=log₂9 log₂3*log₂a=log₂3² log₂3*log₂a=2log₂3 log₂a=2 a=4

aniabb: 9=a^log₂3 obustronnie log₂ log₂9=log₂a^log₂3 2log₂3=log₂a * log₂3 2=log₂a a=2²=4

marek: trochę nie rozumiem jak wyszłaś do takiego rozwiązania log₂3 * log₂a= log₂9 tutaj ten log₂3 jest w wykładniku liczby "a" a się nagle zrobiło mnożenie z tego

aniabb: wzór 4 https://matematykaszkolna.pl/strona/218.html

marek: ok już rozumiem wielkie dzięki dla was Drogie Panie

aniabb: tu lepiej widać https://matematykaszkolna.pl/strona/2813.html

marek: Pozdrawiam

marek: aniabb− tego mi było trzeba bardzo dziękuję za pomoc

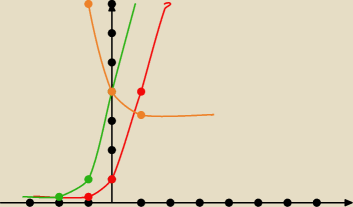
marek: Naszkicuj wykresy g(x)= (x+1) i h(x)=(−x)+3 podaj rozwiazanie równania g(x)=h(x) LEGENDA: czerwony = y=4^x zioleny= y=4^x+1 pomarańczowy = y=4^−x+3 4^x+1=4^−x+3

	1
4x *4=		+3
	4x

czy jeszcze mógłbym liczyć na pomoc w rozwiazaniu tego równania ?

aniabb: jak widać z rysunku x=0 i faktycznie 4=1+3 więc x=0 skoro kazali narysować to warto tego użyć

marek: aż głupio mi się zrobiło że nie spojrzałem na to dziękuję

irena_1:

	1
4*4x=		+3 /*4x
	4x

4*4^2x=1+3*4^x 4^x=t>0 4t²=1+3t 4t²−3t−1=0 Δ=9+16=25

	3−5		3+5
t1=		<0 lub t2=		=1
	8		8

t=1 4^x=1 x=0

marek: irena₁ dziękuję serdecznie to bardzo mi pomogło