Eta lub inny pomocy!!:* magda WROCŁAW: wykaż ze prosta łącząca środki przekątnych trapezu o podstawach a,b (a>b)jest równoległa do podstaw i ma długość równą (a−b)/2

tim: To samo zadanie 19803

magda WROCŁAW: nie u mnie sa środni przekatnych

tim: AAA. Oj przepraszam.

Eta: Witam Ja proponuję tak:

	a +b
IEFI =		−−−− długość linii środkowej trapezu
	2

trójkąty: ABD i NDE są podobne zatem : IENI = ¹₂a także trójkaty: ABC i MFC są podobne: zatem: IMFI = ¹₂a

	a +b		a		b
IEFI − IENI = INFI =>		−		=		= INFI
	2		2		2

	b
podobnie IIEMI =		= INFI
	2

zatem:

	a+b		2b		a +b −2b		a −b
IMNI = IEFI − 2*INFI =		−		=		=
	2		2		2		2

c. b.d.o.

	a −b
odp: IMNI =
	2

Bogdan zapewne poda jeszcze inny sposób

magda WROCŁAW: oo dzięki

Eta:

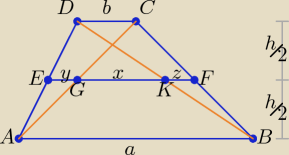Bogdan: Przedstawiam sposób podobny do rozwiązania Ety.

	y		1   h 2		b
Z podobieństwa trójkątów ACD i AGE:		=		⇒ y =
	b		h		2

	z		1   h 2		b
Z podobieństwa trójkątów BCD i BFK:		=		⇒ z =
	b		h		2

y + z = b

	a + b		a + b		a + b		a − b
y + x + z =		⇒ x + b =		⇒ x =		− b =		.
	2		2		2		2

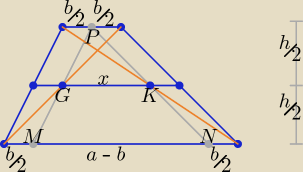Bogdan: Można również tak:

	x		1   h 2
Z podobieństwa trójkątów GKP i MNP:		=		⇒ x = Ua − b}{2}
	a − b		h

Bogdan:

	a − b
Źle się napisało, poprawiam: ⇒ x =
	2

Eta: