trójkąt równoramienny karolina: Dany jest trójkąt równoramienny ABC. Podstawa AB=26cm, wysokość poprowadzona z punktu A wynosi 24cm. Oblicz obwód trójkata ABC, długości odcinków na jakie wysokość CD podzieliła wysokosć AE oraz stosunek pola trójkąta ADS do pola trójkąta CSE, gdzie punkt S jest punktem przecięcia się wysokości. i w sumie to stanęłam na tym że obliczyłam odcinek BE i wyszło mi 10 z twierdzenia pitagorasa, kompletnie nie mam pojęcia co dalej, wpisałam w ten trójkąt okrag ale nie umiem z tego skorzystać

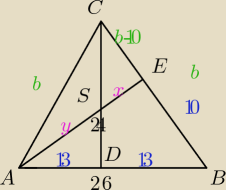
aniabb: pitagoras ΔAEC 24²+(b−10)² = b² 576−20b+100=0 b= 33,8 Obwód ABC = 93,6 wysokość CD (Pitagoras) h²+13²=33,8² ⇒ h = 31,2

	31,2		23,8
ΔCES podobny do ΔCDB		=		x=119/12
	13		x

y=24 − x = 169/12 Pole ADS = 65/12*13 /2 = 845/24 Pole CSE = 23,8*119/12 /2 = 2832,2/24 stosunek pól 845/2832,2 = 4225/14161 = 0,29835

aniabb: https://matematykaszkolna.pl/forum/196154.html