Trójkąty Karola: Dany jeste trójkąt równoramienny ABC. Podstawa AB=26cm, wysokość poprowadzona z punktu A wynosi 24cm. Oblicz obwód trójkata ABC, długości odcinków na jakie wysokość CD podzieliła wysokosć AE oraz stosunek pola trójkąta ADS do pola trójkąta CSE, gdzie punkt S jest punktem przecięcia się wysokości.

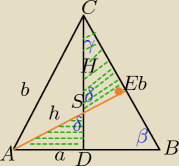
Mila: 1) AB²=EB²+h² 26²=EB²+24² EB²=676−576 |EB|=10 2) W ΔAEC: b²=24²+(b−10)² oblicz

	169		4
b=		=33
	5		5

	4		4
|CE|=33		−10=23
	5		5

3)

1		1
	a*H=		b*h⇔26H=24b
2		2

	169
26H=24*
	5

	156
H=		=31,2
	5

w ΔCDB:

	13
tgγ=
	31,2

W ΔCES:

	SE
tgγ=
	CE

13		SE
	=
31,2		23,8

dokończ obliczenia

	AD		13
ΔADS∼ΔCES (cecha kkk) w skali k=		=
	CE		23,8

spróbuj dalej sama.

aniabb: https://matematykaszkolna.pl/forum/196168.html