trygonometria Licealista D: Witam, jak w takim przypadku y = cos(x−2) obliczyć miejsca zerowe funkcji w przedziale (0;2π>

PW: Funkcja cos(x−2) ma wykres przystający do wykresu funkcji cosx, przesunięty o wektor [2,0]. Po prostu narysować i odczytać odpowiedź z wykresu.

Licealista D: Dobrze, tylko wektor 2 jak mam odzwierciedlić gdy wykresy są w miarach z π? :<

PW: To są liczby, dziedziną funkcji cosx jest zbiór liczb rzeczywistych (liczba π to w przybliżeniu 3,14). Nie należy myśleć o miarach kątów ani geometrycznym sensie, po prostu jest to funkcja, której wykres znamy.

Licealista D: Dobrze, a teraz dla jakiej wartości parametru a istnieje rozwiązanie sin²x + sinx + a = 0 Więc Δ≥0 1−4a ≥ 0 a ≤ ¹₄ i teraz dalej nie wiem.

jikA: Zobacz tutaj 195123.

Licealista D: Rozumiem graficzne rozwiązanie z prostą −m . Ale nie wiem czemu f(1)≥ 0 i f(−1)≥0 sinus przyjmuje wartości od −1 do 1 ale nie mogę dojść do tego czemu tak też jest :<

Prometix: a widziałeś kiedys sinusa wiekszego od 1 albo mniejszego od −1

Licealista D: Nie widziałem ale czemu to ma być większe, bo nic mi nie mówi wykres sinusa do tych warunków f(1)≥0 i f(−1)≥0 . t² + t + m= 0 i teraz f(1) czyli 1² + 1 + m ≥ 0 ale czemu większe hm.

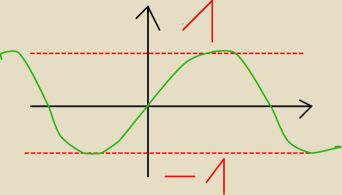
Prometix: Tak mniej wiecej wyglada wykres sinusa wiec jezeli masz rownanie sin²x+sinx+a=0 to pociaga od razu ze ⇒sinx<−1,1> z delty moze ci wyjsc np ze sin bylby rowny 10 i wtedy np dla jakiegos parametru a rownego −110 byloby to prawdziwe rownanie ale sinus nie moze rownac sie 10 stad masz takie zalozenie od razu , i to jest twoja dziedzina innej mozliwosci nie ma

Cusack: popatrz na wykres Mili tutaj: https://matematykaszkolna.pl/forum/195123.html szukamy rozwiązań w przedziale <−1,1> (bo takie wartości przyjmuje sinus) jeżeli f(1) byłoby mniejsze od zera i f(−1)<0 to wtedy nie będzie przecięć wykresu z prostą, czyli brak rozwiązań. A tego nie chcemy

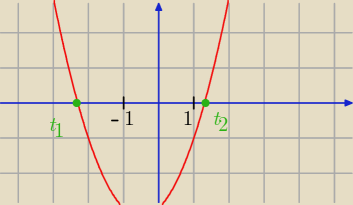
jikA: Jeżeli f(−1) < 0 oraz f(1) < 0 to zobacz jak wyglądał by wykres. t₁ oraz t₂ nie mieszczą się w przedziale [−1 ; 1] a więc brak rozwiązań.

Licealista D: Dobrze, a jakbym chciał obliczyć pierwiastki równania kwadratowego i dać warunek, że muszą być pomiędzy −1 a 1 czyli

	−1 + √1−4m
t1 =
	2

i

	−1 − √1−4m
t2 =
	2

Powinno wyjśc według mojego myślenia a nie wychodzi mi :<

Licealista D: jikA teraz zrozumiałem ale jeszcze zastanawiam się czy z obliczeniem pierwiastków nie dałoby radę rozwiązać.

jikA: Wychodzi też.

	−1 + √1 − 4m
−1 ≤		≤ 1
	2

−2 ≤ −1 + √1 − 4m ≤ 2 −1 ≤ √1 − 4m ≤ 3 0 ≤ 1 − 4m ≤ 9

1
	≥ m ≥ −2
4

lub

	−1 − √1 − 4m
−1 ≤		≤ 1
	2

2 ≥ 1 + √1 − 4m ≥ −2 1 ≥ √1 − 4m ≥ −3 9 ≥ 1 − 4m ≥ 1 −2 ≤ m ≤ 0

	1		1
m ∊ [−2 ;		] ∪ m ∊ [−2 ; 0] ⇒ m ∊ [−2 ;		]
	4		4

Prometix: zobacz : sin²x+sinx+a=0 Δ=b²−4*a*c=1²−4*1*a=(1−4a) to jest moja delta jezeli mam miec w ogole jakies rozwiazanie to wiem że Δ≥0 to jest raczej oczywiste. Ale poza tym te miejsca zerowe które oblicze będą sinusem ( bo mam sinusa w równaniu) wiec dokładam kolejne założenie, że sinx∊<−1;1> wyliczam dla jakiej wartosci Δ≥0 czyli 1−4a≥0 co daje a≤1/4 ( poki co teraz moge mowic w ogole o jakimkolwiek rozwiazaniu ) jednak to rozwiazanie musi siłą rzeczy należeć do przedziału <−1;1> liczysz sinx1=(−b−√Δ)/2a=(−1−√1−4a)/2 i teraz wiesz ze sinx1≥−1 i sinx1≤1 czyli 1≥(−1−√1−4a)/2 oraz −1≤(−1−√1−4a)/2 obustronnie razy 2 i przenosimy odrazu 1 3≥−√1−4a −1≤−√1−4a √1−4a≥−3 √1−4a≤1 widaz ze zeba zaszla nierownosc nr 1 to po prostu wyrazenie pod pierwiatskiem musi byc wieksze od 0 badz rowne (pierwiastek nie moze byc ujemny ) a w nr 2 wyrazenie po pierwiastkiem musi byc po prostu mniejsze badz rowne 1 zatem mam: z nr 1 a≤1/4 z nr 2 a≥0 czyli a∊<0;1/4> teraz analogicznie przyklad drugi czyli drugi pierwiastek sinx2≤1 i sinx2≥−1 nie chce mi sie juz tego tutaj pisac ale otrzymasz : −2≤a i a≤1/4 czyli a∊<−2;1/4> teraz patrzymy na pierwszy warunek czyli Δ≥0 dla a ≤1/4 oczywiscie widzimy ze mamy sinusa ( czyli rozwiazanie gdy a∊<−2;1/4> suma <0;1/4> czyli a∊<−2;1/4>) a ten przedzial spelnia warunek otrzymania jakichkolwiek pierwiastkow rownania sin²x+sinx+a=0 bo miesci sie on w przedziale kiedy Δ≤1/4 czyli odp:a∊<−2;1/4>

Licealista D: Dzięki Wam, teraz już wszystkie podstawowe wątpliwości mam rozwiązane, bo nie lubię z automatu rozwiązywać zadanie jak pojedynczego punktu nie rozumiem