Pole koła wpisanego w trójkąt abc: Odcinek o końcach A = (3, −5) D = (4, −4) jest wysokością trójkąta równobocznego ABC. Oblicz pole koła wpisanego w ten trójkąt. HELP :<

Skipper: ... to policz długość tego odcinka (wysokość trójkąta równobocznego). Dalej już tylko wzorki https://matematykaszkolna.pl/strona/542.html

abc: Długość odcinka = √2 H = √2 P= a²√3/4 H= a√3/2 √2 = a√3/2 a = 2√2/√3 = 2√6/3 P = (24/9)*√3/4 i co dalej?

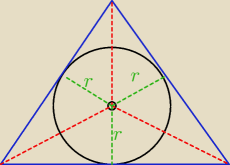
Skipper: jak nie znasz wzoru to zauważ że na pole trójkąta składają się pola trzech trójkątów o wysokości r

abc: Nie wiem, nie potrafię tego zrobić. Czy może mi to ktoś rozwiązać żebym mógł robić kolejne zadania na podstawie tego? Proszę

Ajtek:

	1
Skorzystaj z tego: w Δ RÓWNOBOCZNYM promień okręgu wpisanego w ten Δ jest równy
	3

wysokości tego Δ. Widać to ładnie na rysunku Skipper'a powyżej. To dotyczy tylko Δ RÓWNOBOCZNEGO, pamiętaj o tym .

abc: Okey, czyli r = ¹₃√2. Pole koła = Pi r² = ²₉ PI Zgadza się ?

Ajtek: Zobacz, czy ze wzoru podanego przez Skipper'a wychodzi to samo, to się przekonasz.