Andrzej Kielbasa akante: http://www.zadania.info/d46/512834 wytlumaczy ktos dlaczego dla x nalezacych od (−nieskonczonosc,−2> suma <2,+nieskonczonosc) wierzcholek funkcji wynosi 1,−5? jak mam to zrobic skoro wierzcholek nie nalezy do dziedziny iksow?

akante: czy tutaj informacja jest wazna ale tylko o ramionach? w ktora strone leca ?

jikA: Dlatego tego wierzchołka jak widać na rysunku nie ma i go nie rysujesz. Zapewne tylko sprawdzali czy ten wierzchołek paraboli znajduje się w podanym przedziale.

akante: okey dzieki czyli informacje o kierunku ramion funkcji (po bokach) sa tutaj znaczace tak?

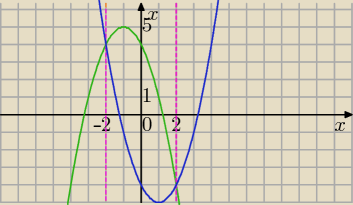
Mila: y=−x²−2x+4 y=x²−4−2x Masz naszkicować wykres funkcji i brać pod uwagę tę część, która jest w dziedzinie. Zwykle rysuje się pierwsze wykresy przerywaną linią. Dla x∊(−2,2) bierzesz część zielonego wykresu poza tym przedziałem część niebieskiego. nie nanoszę koloru bo nie zobaczysz. Moi uczniowie to pięknie rysują.

akante: Dziękuję za pomoc twoi uczniowie? Jesteś nauczycielką? Chyba taka pani z pasją pozatym w jakiej szkole pani uczy ze uczniowie tak pięknie rysują?

akante: kolejne pytanie mamy funkcje f(x)=min(3,x²−5x+7) gdzie min (a,b) oznacza sie nie większą z liczb a,b b)Wyznacz zbiór wartośći funkcji f Wydaje mi sie ze trzeba wyliczyc wspolrzedne ygrekowe wierzcholka x²−5x+7 tej funkcji ale mi sie nie zgadza z odpowiedzią jakieś wskazówki?

jikA: Nie wiem czy dobrze myślę.

	−(−5)
xw =		= 2.5
	2

	3
yw =
	4

	3
ZW = [		; 3]
	4

akante: yw wychodzi ci 3/4? mi wychodzi delta −4

jikA:

	3
Wyszło mi yw =		coś źle obliczyłem?
	4

Krzysiek : https://matematykaszkolna.pl/forum/193989.html Akante zobacz tutaj . Tam podalem Ci link dla wzorow Vietea bo wczoraj pytales o nie

Mila: 1) x²−5x+7=3 x²−5x+4=0 Δ=25−16=9

	5−3		5+3
x=		=1 lub x=		=4
	2		2

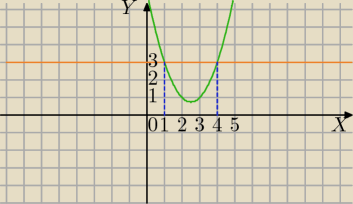
x²−5x+7<3⇔ x∊(1,4) Dla x∊(1,4) f(x)=x²−5x+7 Dla x∊(−∞,1>∪<4,∞) f(x)=3 Wartość największa y_max=3 y_min=y_w paraboli

	5
xw=
	2

	5		5		3
yw=(		)2−5*		+7=
	2		2		4

	3
Zwf=<		,3>
	4

akante: DZIEKUJĘ

Mila: