geometria
Dariusswwe: dany jest trapez prostokątny: wiedząc że górna podstawa jest 2 razy dłuższa od wysokości
trapezu , krótsza przekątna ma długość 3 √5 oblicz pole tego trapezu oraz kąt nachylenia
dłuższej przekątnej do dolnej podstawy tego trapezu... drugie ramię ma długość √11
25 sie 17:33
Kuba: ramię czy jednak druga przekątna ma długość?;>
25 sie 17:44
Dariusswwe: ramię − te które nie jest wysokością ma długość √11
25 sie 17:45
evil_woodworm:
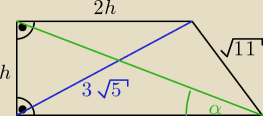
25 sie 17:52
Dariusswwe: dokładnie tak
25 sie 17:54
Bogdan:
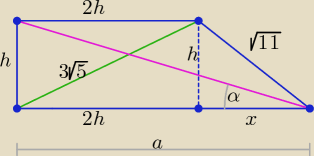
h
2 + 4h
2 = 45 ⇒ 5h
2 = 45 ⇒ h
2 = 9 i h > 0 ⇒ h = 3
2h = 6
x =
√11 − 9 =
√2
a = 2h + x = 6 +
√2
| | 1 | | 3 | |
Pole P = |
| (6 + √2 + 6)*3 = 18 + |
| √2 [j2] |
| | 2 | | 2 | |
| | h | | 3 | | 6 − √2 | | 18 − 3√2 | |
tgα = |
| = |
| * |
| = |
| ≈ 0,4046 |
| | a | | 6 + √2 | | 6 − √2 | | 34 | |
α ≈ 22
o
25 sie 21:43
Dariusswwe: Bogdan a takie coś nie może być...
2h
2 + h
2 = 3
√5 2
czyli 3h
2 = 45 /:3
h
2 = 15
h=
√15
idąc dalej:
h
2+x
2 =
√112
√152 + x
2 = 11
x
2 = 11 − 15
x
2 = −4
x =
√−4
x = 2
i dalej liczę pole i wychodzi 45... może tak być

25 sie 21:50
tim: √−4 ≠ 2... Tak a propos...
Zauważ, że macie inne wysokości...
25 sie 21:57
Dariusswwe: zauważyłem ten pierwiastek

25 sie 22:00
Bogdan:
Nie 2h2 + h2, ale (2h)2 + h2 = 4h2 + h2 = 5h2
25 sie 22:45
Dariusswwe: rozumiem już....a powiedz mi czy zadanie 9 mam dobrze rozwiązane

patrz wyżej
25 sie 22:47
Bogdan:
Zadanie 9 tu rozwiązałem
19217
25 sie 23:02

 h2 + 4h2 = 45 ⇒ 5h2 = 45 ⇒ h2 = 9 i h > 0 ⇒ h = 3
2h = 6
x = √11 − 9 = √2
a = 2h + x = 6 + √2
h2 + 4h2 = 45 ⇒ 5h2 = 45 ⇒ h2 = 9 i h > 0 ⇒ h = 3
2h = 6
x = √11 − 9 = √2
a = 2h + x = 6 + √2


 patrz wyżej
patrz wyżej