zadania z poprawki-- matura 2009 Dariusswwe: Witam...właśnie wróciłem z poprawki z matmy podstawowej... za chwilkę wstawię zadanka które pamiętam...proszę o rozwiązania

Dariusswwe: 1) było trzeba rozpisać liczby i doprowadzić je do postaci 2 do potęgi x... 2) średnia arytmetyczna zarobków w pewnej firmie na 30 pracowników wynosiła 1950zł... po tym jak zwolniono 2 pracowników średnia ta wzrosła o 4 %...trzeba było obliczyć ile zarabiali ci pracownicy wiedząc że jeden z nich zarabiał 76% pensji drugiego... 3) f kwadratowa dana jest wzorem f(x) = ax²+bx+c ....nie pamiętam dalej ale trzeba było wyliczyć współczynniki > moim zdaniem najtrudniejsze zadanie 4) rozwiąż równanie x³ + 3x = 3 − x² chyba tak 5) dany jest trapez prostokątny: wiedząc że górna podstawa jest 2 razy dłuższa od wysokości trapezu , krótsza przekątna ma długość 3 √5 oblicz pole tego trapezu oraz kąt nachylenia dłuższej przekątnej do dolnej podstawy tego trapezu 6) dany był ciąg arytmetyczny , w którym po obliczeniu a1 wyszło mi 9 trzeba było obliczyć 8 wyraz bodajże wiedząc że suma pierwszych trzech wyrazów była 2 razy mniejsza od 3 następnych wyrazów tego ciągu 7) ciąg geometryczny malejący o wyrazie a1= 27 i a5= 1/3 i trzeba było obliczyć sumę pierwszych 3 wyrazów 8) było stożek którego wysokość równa się 8... a stosunek pola pow bocznej do pola podstawy równa się 5:3... trzeba było obliczyć objętość stożka 9) czy istnieje taki kąt ostry że sinL = 2/3 a tg = 5 należało to zbadać 10) wykres funkcji był i należało odczytać własności 11) były podane 4 punkty i z tych punktów wyszedł trapez...pozniej podano dodatkowy punkt i wyszedł trójkąt równoramienny...należało to udowodnić i napisać równanie symetralnej tego trójkąta 12) nie pamiętam niestety

Dariusswwe: 12) związane ze średnią arytmetyczną i średnią ważoną

Ania : Witam, pamiętasz może ile wyszło w 1 zadaniu a i b?

Dariusswwe: witam... m i n mi wyszło 2⁴ a w b... że da się podzielić przez 3 bodajże 1008... a Tobie jak wyszło

Ania : m nie pamiętam, a n tak samo, w podpunkcie b tak samo

Dariusswwe: a pole trapezu i kąt nachylenia ile ci wyszedł....mi pole 45... a kąt 57

Ania : kąta zapomniałam obliczyc:( a pole coś z pierwiastkami, nie pamiętam dokładnie... a zadanie ze stożkiem?

Dariusswwe: to ze stożkiem obok tego z funkcją kwadratową najbardziej zepsułem... tu raczej będzie 0 a z ciągami jak sobie poradziłaś

bulaj: w 5 zadaniu zapomnieles dodac ze ramie ma √11

Ania : W 6 a1=9, zapislam zależnośc i dalej brak pomyslu:( 7. ułożyłam uklad rownan i chyba q= 4, i podstawiłam do wzoru na Sn, a Tobie? a w 12 jaka srednia, i ktora metoda?

Dariusswwe: tak jest zgadza się

Dariusswwe: w zad 6 a1=9 i policzyłem tak jak tu.. https://matematykaszkolna.pl/forum/19216.html w 7 q = 3 i niby dobrze mi wyszło a w 12 lepsza 2 metoda bo Adam dostał by 5 xD jak zapisałaś to równanie co było do wyliczenia

paula: a za ile bylo pkt pierwsze zadanie

Dariusswwe: za pierwsze 4 pkt

Dariusswwe: piszcie rozwiązanie te co wiecie

Ania : Tak, przepraszam w 7 q=3, 0.5(a1+a2+3)=a4+a5+a6 chyba

paula: a Q nie wyszlo minus 3

Dariusswwe: a jak zrobiliście 4 9 i 11 patrz do góry

Dariusswwe: Q nie mogłoby być −3 bo wówczas ciąg nie był by malejący tylko naprzemienny... sprawdzałem to

Ania : A w zadaniu z trapezem jak wyszla wam wysokosc, golna i gorna podstawa?

Ania : właśnie z tym q nie jestem pewna czy powninno byc 3, a −3 nie może byc, bo q>0

Dariusswwe: z trapezem wysokość mi wyszła √15 górna podstawa 2 √15 a dolna podstawa 4 √15 .... pole 45 a kąt 57... a wam

Dariusswwe: a z tym q to powinno być q = 1/3

paula: a co bylo za 2 zadanie

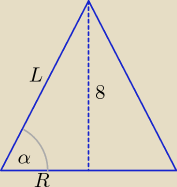
Bogdan: Zadanie ze stożkiem, szkic rozwiązania.

PB

5

πRL

5

L

5

R

3

=

⇒

=

⇒

=

⇒

=

.

PP

3

πR2

3

R

3

L

5

α ∊ (0, 90^o)

	R		3		4
cosα =		⇒ cosα =		⇒ sinα = √1 − cos2α = √1 − 9/25 =		.
	L		5		5

	8		4		8
sinα =		⇒		=		⇒ L = 10
	L		5		L

R = √10² − 8² = √100 − 64 = √36 = 6

	1
Objętość V =		π*62*8 = 96π [j3]
	3

paula: a jak zrobiliscie 4

paula: i za ile bylo pkt?

Bogdan: Zadanie 4 na pewno nie jest: x³ + 3x = 3 − x². Raczej jest: x³ + 3x = 3 + x². x³ − x² + 3x − 3 = 0 ⇒ x²(x − 1) + 3(x − 1) = 0 ⇒ (x − 1)(x² + 3) = 0 x = 1. x² + 3 > 0 dla każdej wartości x∊R.

Bogdan: Zadanie 7. Szkic rozwiązania: Ciąg geometryczny (a_n): a₁ = 27 = 3³

	1		1
a5 =		= 3−1 ⇒ 3−1 = 33*q4 / : 33 ⇒ q4 = 3−4 =
	3		81

	1		1		1
q4 −		= 0 ⇒ (q2 −		)(q +		) = 0 ⇒
	81		9		9

	1		1		1
⇒ (q −		)(q +		)(q +		) = 0
	3		3		9

	1		1
q =		lub q = −
	3		3

	1		1
a1 = 27 *		= 9 i a2 = 9 *		= 3
	3		3

lub

	−1		−1
a1 = 27 *		= −9 i a2 = −9 *		= 3
	3		3

S₃ = 27 + 9 + 3 = 39 lub S₃ = 27 − 9 + 3 = 21

Bogdan: Zadanie 9.

	2		sinα		2   3		2
sinα =		, tgα = 5 ⇒		= 5 ⇒ cosα =		=
	3		cosα		5		15

	4		4		900 + 36		936
sin2α + cos2α =		+		=		=		≠ 1
	9		225		9*225		2025

Nie istnieje taki kąt α

Bogdan: Jaka jest treść zadania z trapezem? W podanej wyżej treści coś jest nie tak.

Bogdan: Zadanie 2, szkic rozwiązania. S₃₀ − suma zarobków 30 pracowników, S₂₈ − suma zarobków 28 pracowników.

S30
	= 1950 ⇒ S30 = 30*1950.
30

S28
	= 1,04*1950 ⇒ S28 = 28*1,04*1950.
28

S₃₀ − S₂₈ = 30*1950 − 28*1,04*1950 = 1716. x − zarobek I pracownika 0,76x − zarobek II pracownika x + 0,76x = 1716 ⇒ 1,76x = 1716 ⇒ x = 975 i 0,76x = 741.

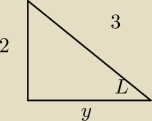
Dariusswwe: czy 9 zadanie mogłem rozwiązać tak? : sinL = 2/3 z twierdzenia pitagorasa doliczam y= √5 następnie tg L = 2/y czyli 2/ √5 po usunięciu niewymierności mam że tgL = 2 √5 / 5... a więc taki kąt nie istnieje... czy takie rozwiązanie jest poprawne

Dariusswwe: dany jest trapez prostokątny: wiedząc że górna podstawa jest 2 razy dłuższa od wysokości trapezu , krótsza przekątna ma długość 3 √5 oblicz pole tego trapezu oraz kąt nachylenia dłuższej przekątnej do dolnej podstawy tego trapezu... drugie ramię ma długość √11

Ania : ile jest puntów za zadanie 11?

Dariusswwe: chyba 4

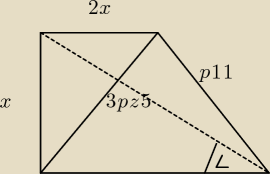
Dariusswwe: dany jest trapez prostokątny: wiedząc że górna podstawa jest 2 razy dłuższa od wysokości trapezu , krótsza przekątna ma długość 3 √5 oblicz pole tego trapezu oraz kąt nachylenia dłuższej przekątnej do dolnej podstawy tego trapezu... drugie ramię ma długość √11

Dariusswwe: hejka czy moje rozwiązanie zadanie 9 jest poprawne

Bogdan: Do Dariusswwe Pomysł na rozwiązanie zadania 9 jest dobry, wypadało oznaczyć boki: 2x, 3x, x > 0, a nie 2, 3. y = √9x² − 4x² = x√5

Dariusswwe: ale wykonując takie rozwiązanie mogę liczyć na jakieś punkty bodajże 3 do zdobycia?

Bogdan: Tak, otrzymasz 1 punkt mniej.

Maćko: Zadanie 9 Z tw. Pitagorasa x²+(2x)²=(3√5)² zatem wysokość jest równa 3, a krótsza podstawa 6. Teraz drugi raz tw Pitagoras 3²+a²=√11², gdzie a to ten mały odcinek z dłuższej podstawy jak się narysuje wysokość z wierzchołka kata rozwartego a=√2 Stąd pole 0,5(6+6+√2)*3

majka: Maćko, zgadza się! wynik ten sam co u mnie

Eta: Przeglądając rozwiązania zadań, zauważyłam małą nieścisłość w zad 7 Bogdan przeoczył ...... ciąg ma być malejącym zatem przyjmujemy zgodnie z treścią , że q= ¹₃ bo dla q= −¹₃ −−− ciąg jest przemienny więc jest tylko jedna wartość S₃ , S₃ = 39

Bogdan: Rzeczywiście nie uwzględniłem warunku o ciągu malejącym i dlatego podałem we wstępie tego zadania, ze jest to szkic rozwiązania, a nie rozwiązanie. Powinienem jednak na końcu dopisać: "teraz trzeba uwzględnić warunki zadania". Dziękuję Eto za uzupełnienie, bo porządek musi być

Dariusswwe: Hejka! czy sądzicie że otrzymam jakieś punkty za rozwiązanie z trygonometrii (9) Bodajże 3 pkt do zdobycia....moje rozwiązanie jest w tym poście troszkę wyżej...proszę o opinie

Alinka: Myślę, że Ci uznają to rozwiązanie, ale czy za całe 3 pkt to nie ręczę.