pola figur Kurczab Świda Patri: Było już ale chcę dopytać. 9.147. W kole z jednego punktu okręgu poprowadzono dwie cięciwy o długości 6 cm każda. Wiedząc, że utworzyły one kąt 60°, oblicz pole części koła zawartej między tymi cięciwami. w odpowiedziach jest wynik 2(3√3 + 2π) i nie bardzo rozumiem czemu brana jest mniejsza część koła a nie większa. Przecież to nie powinno być zalezne od tego jak zrobię swój rysunek, a jednak zalezy? Tu link do zadania: https://matematykaszkolna.pl/forum/19104.html

Mila: Twoje rozwiązanie podane w linku, jest błędne, spróbuj narysować okrąg o promieniu 6, nie pokryje się z łukiem między cięciwami. Po kolacji mogę dalej objaśniać.

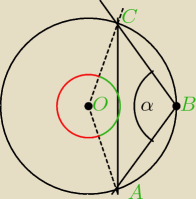
Patri: To w linku to nie jest moje rozwiązanie, ale wyliczenia prowadzą do dobrego wyniku Tam nic nie jest napisane o tym, ze promień ma być 6, no i nie jest. No ale załączam rysunek jaki sama zrobiłam w zeszycie. Trójkąt u mnie nie jest faktycznie równoboczny, bo to rysunek poglądowy i w sumie nie powinien mieć większego znaczenia, bo ważne są obliczenia. Chodzi o te dwa kąty − czerwony i zielony. U mnie pole pomiędzy cięciwami to wycinek koła o kącie 240 − czerwonym − plus pole czworokąta ABCO. O ile pole czworokąta wyszło mi dobrze, o tyle kąt 240 okazał się kątem 120, gdy rysunek zrobić nieco inaczej.

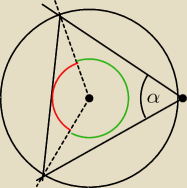
Patri: Gdyby rysunek zrobić inaczej, rzecz stałaby się oczywista. Pytanie moje dotyczy więc tego, dlaczego tak istotne jest robienie dobrego rysunku w miejsce poglądowego i jak unikać takich błędów. Mi wyszło 2(3√3*4π) a w odpowiedzi jest 2(3√3*2π). Smacznego

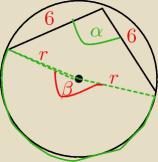
Mila: Niezależnie jak niedokładny rysunek, to kąt β=2α=120 i szkic poprawiam, albo rozumiem, że jest niedokładny i liczę. Kąt wpisany oparty na tym samym łuku co środkowy jest dwa razy mniejszy od środkowego. (kąt środkowy dwa razy większy). Zatem w żadnym wypadku nie jest to kąt o mierze 240. Dowolność szkiców ma swoje granice.

Patri: Super, twierdzenie, o kącie wpisanym i środkowym przekonało mnie absolutnie. W porządku. Dziękuję Ci bardzo za odzew i wyjaśnienie.

Mila: