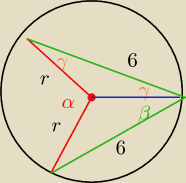
 β=60 stopni zielony kąt
α=120 stopni
2γ=β
γ=30
mozemy policzyć długość promienia z funkcji trygonometrycznych
r=2√3
teraz podzieliłem szukae pole na trzy części dwa trójkąty i część okręgu o promieniu r i kącie
120
liczymy pole trójkąta
P1=1/2*a*h
a=6
h=√3 też z funkcji trygonometrycznych
P1=3√3
P2−pole okręgu o kącie 120
P2=120/360* π*r2=4π
P=2P1+P2
P=6√3+4
P=2(3√3+2π)
β=60 stopni zielony kąt
α=120 stopni
2γ=β
γ=30
mozemy policzyć długość promienia z funkcji trygonometrycznych
r=2√3
teraz podzieliłem szukae pole na trzy części dwa trójkąty i część okręgu o promieniu r i kącie
120
liczymy pole trójkąta
P1=1/2*a*h
a=6
h=√3 też z funkcji trygonometrycznych
P1=3√3
P2−pole okręgu o kącie 120
P2=120/360* π*r2=4π
P=2P1+P2
P=6√3+4
P=2(3√3+2π)

 Można też rozwiązać tak ; ( bez korzystania z funkcji tryg.
trójkąt wyznaczony przez dany punkt i końce cięciw jest równoboczny o boku = 6
promień okręgu opisanego na tym trójkącie jest "r"
Można też rozwiązać tak ; ( bez korzystania z funkcji tryg.
trójkąt wyznaczony przez dany punkt i końce cięciw jest równoboczny o boku = 6
promień okręgu opisanego na tym trójkącie jest "r"
| a√3 | ||
gdzie r =23hΔ = 23* | ||
| 2 |
| 6√3 | ||
więc r = 23* | = 2√3
| |
| 2 |
| πr2*120o | a2√3 | |||
P= | + 23* | |||
| 360o | 4 |
| 36√3 | ||
P= 13*π*(2√3)2 + 23* | = 4π +6√3= 2(3√3 +2π)
| |
| 4 |