znaleźć ekstrema funkcji Krystian: znaleźć ekstrema funkcji f'(x)=x²*e⁻x zupełnie nie mam pojęcia jak to rozwiącać (x kwadrat razy e do potęgi minus x)

Krzysiek: https://matematykaszkolna.pl/strona/387.html

Krystian: zapoznałem sie z tym: pochodna to: −e⁻x(x−2)x nie mam pojęcia jak policzyć z tego Δdelte aby stworzyć postać iloczynową

Mila: f(x)=x²*e^−x to wzór Twojej funkcji?

asdf:

	x
x*e−x =		.. to samo x ∊ R (mianownik nigdy nie osiągnie zera)
	ex

licze pochodną: y' = x*e^−x = x'e^−x + e^−x*(−x)'*x = e^−x − e^−x*x =e^−x(1−x) przyrownuje do zera: y'=0 e^−x(1−x) = 0 // e^−x, tutaj mozna jedynie mnożyć ludz bielić przez liczbę, która wiadomo,

	1
że jest DODATNIA, a to, że e−x jest zawsze dodatnie (patrz wykres		, ale mozesz mi
	ex

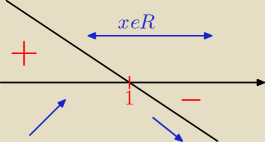
w tej kwesti zaufać ) 1−x = 0 x=1 rysujesz od prawej strony z dołu − znak ujemny przy x po redukcji. Już sam określ czy to jest minimum czy maksimum

asdf: widze, że źle przepisałem, nie x, tylko x² − pochodną policzysz, zrobisz podobnie i będzie dobrze

Krystian: @Mila:nie xe⁻x super! dzięki na przykładach dużo łatwiej się nauczyć, jednak mam jeszcze kłopot z takimi oto przykładami: f(λ)=x*lnx f''(x)= lnx +1 f(y)=xe⁻x f(x)= x²*e⁻x

Mila: Krystian napisz całą treść zadania. Jaki kłopot, nie wiadomo co chcesz policzyć.

Krystian: Musze policzyć ekstremum funkcji i w poprzednim poście wypisałem przykłady.