wyznacz
misak: Wyznacz na prostej y=x punkt C , aby suma kwadratów jego odległości od A (1;−2) i B(−2;1) była
najmniejsza
8 mar 17:23
konda: Punkt C leży na prostej y=x, więc ma współrzędne C=(x,x)
|BC|2 + |AC|2 ⇒ jak najmniejsze
Ze wzoru na odległość dwóch punktów oblicz tą równość i powstanie równanie kwadratowe, o
ramionach skierowanych ku górze. Wtedy najmniejsza wartość przypadnie w wierzchołku
8 mar 17:39
StaryRafiki: Czesc,
Skoro punkt C jest na prostej y=x to jest postaci (a,a).
Skoro suma kwadratow odleglosci ma byc najmniejsza, a one leza w tej samej odleglosci od
prostej, to leza w tej samej odleglosci od punktu, czyli dla nas wazny jest kwadrat jednej z
tych odleglosci.
Bo szukamy jego podwojenia.
Zadanie sprowadza sie do wsadzenia 2 punktow do wzoru na dlugosc wektora. Pierwszy punkt to
jeden z A,B drugi to (a,a), pozniej likwidujesz pierwiastek kwadratem(tresc zadania)
Zostaje Ci rownanie kwadratowe i sprawdzasz gdzie parabola ma wartosc min.
Jesli masz z czyms problem rob rys

Pozdrawiam,
8 mar 17:52
PW: Pomocnicze pytanie: A jakie przekształcenie płaszczyzny na płaszczyznę zamienia współrzędne
punktu, to znaczy punktowi (x,y) przyporządkowuje punkt (y,x)?
8 mar 19:16
misak: nie rozumiem co tu mam zrobić:(
8 mar 19:43
PW: Słyszałeś o symetrii osiowej o osi y=x?
8 mar 19:48
misak: nie chyba nie ..
8 mar 19:51
Mila:
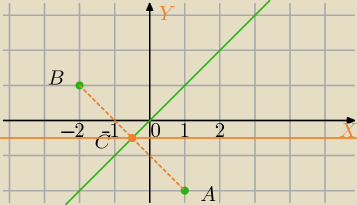
A (1;−2) i B(−2;1)
k: y=x
C∊k⇔C=(c,c)
|AC|
2=(1−c)
2+(−2−c)
2
|BC|
2=(−2−c)
2+(1−c)
2
f(c)=(1−c)
2+(−2−c)
2+(−2−c)
2+(1−c)
2
f(c)=4c
2+4c+10 najmniejsza wartość w wierzchołku paraboli
II sposób
skorzystać z tego że punkty A i B są symetryczne względem prostej y=x,
zatem są równo odległe od prostej i AB⊥k,
punkt C jes punktem przecięcia prostej y=x i prostej AB
AB: y=−x+b i A∊do prostej
−2=−1+b⇔b=−1
AB: y=−x−1
−x−1=x
−2x=1
8 mar 22:25
8 mar 22:26
 Pozdrawiam,
Pozdrawiam,
 A (1;−2) i B(−2;1)
k: y=x
C∊k⇔C=(c,c)
|AC|2=(1−c)2+(−2−c)2
|BC|2=(−2−c)2+(1−c)2
f(c)=(1−c)2+(−2−c)2+(−2−c)2+(1−c)2
f(c)=4c2+4c+10 najmniejsza wartość w wierzchołku paraboli
A (1;−2) i B(−2;1)
k: y=x
C∊k⇔C=(c,c)
|AC|2=(1−c)2+(−2−c)2
|BC|2=(−2−c)2+(1−c)2
f(c)=(1−c)2+(−2−c)2+(−2−c)2+(1−c)2
f(c)=4c2+4c+10 najmniejsza wartość w wierzchołku paraboli