wyznacz misak: Wyznacz na prostej y=x punkt C , aby suma kwadratów jego odległości od A (1;−2) i B(−2;1) była najmniejsza

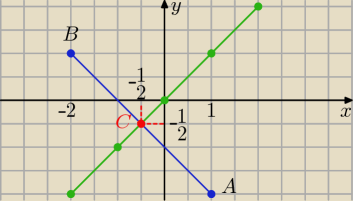
KobiEta: C€ y=x to C(x,x) f(x)=|AC|²+|BC|²−−−− osiąga minimum f(x)= (x−1)²+(x+2)²+(x+2)²+(x−1)² =.... = 4x²+4x+10 −− parabola ramionami do góry czyli f(x) osiąga minimum dla odciętej wierzchołka

	−4		1
dla x=		=−		−−
	8		2

	1		1
odp: C(−		, −		)
	2		2

PW: No i popatrz − gdybyś domyślił się, że punkty A i B są symetryczne względem prostej y=x (co Ci podpowiadałem), to odpowiedź miałeś prawie bez rachunków − wiadomo że dla punktów symetrycznych względem osi − najbliższy na osi jest środek odcinka AB, czyli punkt C AC najmniejszy z możliwych, BC też, a więc i suma kwadratów najmniejsza. Ja tak podpowiadam pod kątem egzaminu maturalnego − najważniejszy jest czas, którego jest zawsze za mało. Dobrze jest znaleźć taki sposób, który pozwoli uniknąć skomplikowanych rachunków i uzasadnień (a i możliwości pomyłki z tym związanej).

Eta:

Eta: Sposób rozwiązania , tak na wszelki wypadek, gdyby punkty nie były symetryczne względem danej prostej