6 mar 19:43
bash: dobrze

6 mar 19:44
Eta:
ok


6 mar 19:45
PuRXUTM: dziękuje

6 mar 19:46
bash: cześć
Eta 
6 mar 19:47
Eta:
6 mar 19:52
Eta:
Witam obu
Panów 
6 mar 19:52
PuRXUTM: Witaj Eto

Dokładnie taki sam mam rysunek

Teraz męczę się z 2, coś dla ICSP

6 mar 19:59
Eta:
2/ W(−1) =.........
podziel Hornerem i zobaczysz ,jak łatwo pójdzie

(x+1)
2(x
2−2)
2≤0 ⇒ .................
6 mar 20:03
PuRXUTM: kurde źle sobie tabelkę napisałem... dziękuje

6 mar 20:34
PuRXUTM: A podpowiesz Eto co w 3 ? bo nie mogę ruszyć
6 mar 20:49
Patryk:
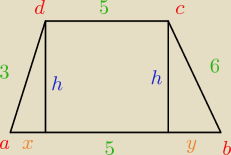
x+y=6
y=6−x
x
2+h
2=9
(6−x)
2+h
2=36
moze to
6 mar 20:54
Saizou : to ja jeszcze pogrupuję ten wielomian
x6+2x5−3x4−8x3+8x+4=
x6+2x5+x4−4x4−8x3+8x+4=
x4(x2+2x+1)−4x4+4−8x3+8x=
x4(x+1)2−4(x4−1)−8x(x2−1)=
x4(x+1)2−4(x2−1)(x2+1)−8x(x2−1)=
x4(x+1)2+(x2−1)(−4x2−8x−4)=
x4(x+1)2−4(x2−1)(x2+2x+1)=
x4(x+1)2−4(x2−1)(x+1)2=
(x+1)2(x4−4x2+4)=
(x+1)2(x2−2)2
6 mar 20:56
Eta:
3/ założenie x€(0,6)
porównaj h
2
36−(6−x)
2=9−x
2 i dokończ......... x=...
to: h=.... i P=....

6 mar 20:59
PuRXUTM: a 4 ? kurcze próbowałem ze wzoru na sumę i róźnicę cosinusów ale nic mądrego nie wychodzi...
6 mar 21:17
PuRXUTM: dziękuje Saizou, Patryk, Eta

6 mar 21:19
Eta:
4/ cos(α+β)=.... i cos(α−β)=....
i każdy podnieś do kwadratu , ładnie się wyredukuje
następnie za: sin
2x = 1−cos
2x
otrzymasz ostatecznie :
cosx(cosx−1)=0

6 mar 21:26
PuRXUTM: | | 16 | |
dziękuje  W 5 ma być sinα= |
| |
| | 33 | |
6 mar 21:41
PuRXUTM: | | π | | π | |
a w tym 4 to wychodzi x= |
| +2kπ v x=− |
| +2kπ v x=2kπ, k∊C ? |
| | 2 | | 2 | |
6 mar 21:47
Eta:
| | π | |
4/ x= |
| +kπ v x= 2kπ ,k€C |
| | 2 | |
6 mar 21:49
PuRXUTM: no to to samo, kurcze ciężkie te zadania... kolejnego (6) też nie umiem...
6 mar 21:51
6 mar 22:02
PuRXUTM: dzięki

6 mar 22:35
Mila: 10 komuś nieopatrznie zrobiłam, nie zauważyłam, że już na info są próbne matury.
Ładne zadania.
Dobrze, że je rozwiązujesz. Im więcej teraz potu, to lżej będzie na maturze.
Eto, nie rozwiązujmy tych próbnych, matur − podpowiadamy i sprawdzamy?
6 mar 23:55
Eta:
Ja nie rozwiązuję

Wczoraj sama rozwiązałaś zad. z równoległobokiem .
Miłych snów

7 mar 00:06
7 mar 00:12
Mila: Oj, rozwiązałam, ale dlatego, że przeoczyłam maturki próbne.
Również miłych snów. Dobranoc:

7 mar 00:15
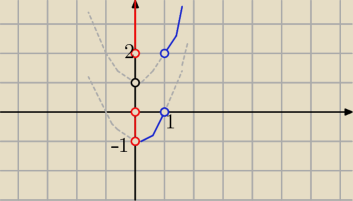
 http://www.zadania.info/d1507/76892
W zadaniu 1 wyszło mi że Zw=(−1;0) U (2;+∞) dobrze ?
http://www.zadania.info/d1507/76892
W zadaniu 1 wyszło mi że Zw=(−1;0) U (2;+∞) dobrze ?







 Dokładnie taki sam mam rysunek
Dokładnie taki sam mam rysunek  Teraz męczę się z 2, coś dla ICSP
Teraz męczę się z 2, coś dla ICSP 
 (x+1)2(x2−2)2≤0 ⇒ .................
(x+1)2(x2−2)2≤0 ⇒ .................

 x+y=6
y=6−x
x2+h2=9
(6−x)2+h2=36
moze to
x+y=6
y=6−x
x2+h2=9
(6−x)2+h2=36
moze to



 W 5 ma być sinα=
W 5 ma być sinα=

 Wczoraj sama rozwiązałaś zad. z równoległobokiem .
Miłych snów
Wczoraj sama rozwiązałaś zad. z równoległobokiem .
Miłych snów
