Nierówność Ania: Rozwiąż nierówność 4x³−3x−1>0

aniabb: według tego https://matematykaszkolna.pl/strona/1401.html wstawiając 1 bo 4*1−3*1−1=0

aniabb: wynik 4x³−3x−1 = (x−1)(4x²+4x+1) = (x−1)(2x+1)² zatem (x−1)(2x+1)²>0 i rysujemy "wężyk"

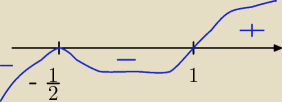
aniabb: odp x>1

adaminh: 4x³−4x+x−1>0 4x(x²−1)+(x−1)>0 4x(x−1)(x+1)+(x−1)>0 (x−1)(4x²+4x+1)>0 I masz rownanie kwadratowe.

Ania: To nie o to chodzi Po rozwiązaniu mamy (x−1)(4x²+4x+1)>0 i teraz mam wątpliwości x=1 oraz x= −¹₂ i to jest pierwiastek równania kwadratowego podwójny. mamy (x−1) (x+¹₂)²>0 i teraz mam wątpliwości co do odpowiedzi Prosze o dokończenia

Ania: ok dziękuję o to chodziło

aniabb: dokończeniem jest rysunek

Ania: dziękuję

Basia: 4x² + 4x + 1 ≠ (x+¹₂)² 4x² + 4x + 1 = 4(x+¹₂)² = (2x+1)² masz więc 4(x−1)(x+1/2)² > 0 ⇔ (x−1)(x+1/2)² > 0 ⇔ x−1>0 i x+1/2≠0 bo (x+1/2)²≥0 dla każdego x i to jest dokładnie to co aniabb Ci napisała