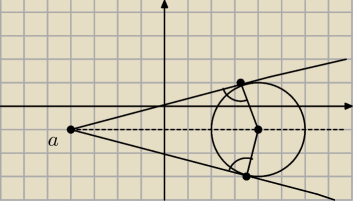
mega trudne Kipic: Dla Hardcora mam pytanie dosyć czesto to sie pojawia na maturach i moje pytanie jest takie <RYSUNEK> jak okreslic rownania stycznych tego okregu jesli wiadomo ze a (−4,−1) a SRODEK OKREGU TO (4,−1) i promien ma 2 Prosze o wskazowki

Kejt: pochodną

Dominik: A = (−4, −1) rownanie prostej y = ax + b −4a + b = −1 b = −1 + 4a y = ax + 4a − 1 prosta prostopadla do tej prostej to

	1
y = −		x + 4a − 1
	a

ta prosta przechodzi przez srodek okregu (4, −1)

	1
−1 = −		* 4 + 4a − 1
	a

wyznacz a i podstaw do rownania prostej, koniec zadania.

Kipic: pochodną . niemam o nich pojęcia a nie przypadkiem to zadanie się na wktrorach robiło ?>

Kejt: hah, możliwe.. nie wiem żartuję sobie..

Dominik: tylko jak teraz to licze to cos mi sie nie zgadza, musialem sie gdziec walnac. ma ktos pomysl.

Kejt: znalazłam coś podobnego: https://matematykaszkolna.pl/forum/6386.html

Kipic: No własnie Dominik ja to robiłem już tyloma sposobami że szok a ani razu nie trafiłem w prawidłową odp jedynie jak podstawiam punkty to wtedy ladnie wychodzi ale akurat w tym przykladzie ladnie je widac ale sa takie w których niema tak ładnie punktów w których ( a;b) sa liczbami całkowitymi ale jakby tutaj mozna bylo wyczytac punty to wtedy tylko do wzoru i juz Ma ktos pomysł jak to zrobic prosze o pomoc

Kipic: no tak Kejt ale to chya jednak inaczej się robi . bo z tego linku trzeba sie strasznie duzo napisac

Dominik: @Kejt, tamto zadanie jest o tyle latwiejsze ze znamy dlugosc promienia.

Dominik: latwiej jest je zrobic wg mnie ze wzoru na odleglosc punktu od prostej, a nie liczenia rownan kwadratowych z parametrem (paskudne rachunki).

Patryk:

	√15
czy równanie jednej ze stycznych to y=		+b ? b specialnie nie obliczam
	15

Patryk: x zabrakło

Kejt: ja i tak przychylam się do liczenia pochodnej..

Dominik:

	1		1
proste maja rownania y =		x i y = −		x − 2
	4		4

ale jak do tego dojsc − to jest pytanie. bo wywnioskowac z wykresu kazdy potrafi.

Dominik: @Kejt, czego pochodna chcesz tu liczyc?

Patryk: a wg mnie mają tyle co ja napisałem

Dominik: to dawaj rachunki

Kipic: nie

Dominik: @Kipic − z ciekawosci, dobrze zgadlem rownania prostych?

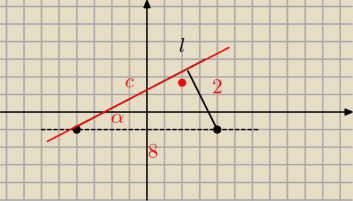
Patryk: 2/c=tgα=a

Kipic: To się jakos na wektorach robilo chyba

Kipic: No Dominik ta jest w odp

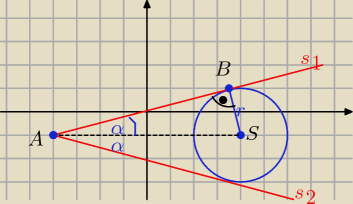
Eta: |AS|= 8 , |BS|=2 |AB|= 2√15

	r
tgα=		=.....
	|AB|

tgα=a s₁: y= a(x+4)−1 s₂= −a(x+4)−1

Kejt: ok, cofam to co pisałam.

Dominik: dopiero doczytalem, ze w poleceniu mamy dana dlugosc promienia! zatem zadanie jest banalne. rownanie stycznej jak napisalem wyzej y = ax + 4a − 1 ax − y + 4a − 1 = 0 ze wzorku na odleglosc punktu od prostej

|4a + 1 + 4a − 1|
	= 2
√a2 + 1

|8a| = 2√a² + 1 64a² = 4a² + 4 60a² = 4 15a² = 1

	1
a2 =
	15

	√15		√15
a =		v a = −
	15		15

nie mam pojecia czemu otrzymuje to co Patryk. gdzie jest blad?

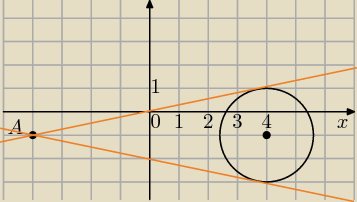
Mila: Można tak: s: y=ax+b i A=(−4,−1)∊s −1=−4a+b b=4a−1 s: y=ax+4a−1 przekształcam do postaci ogólnej ax−y+4a−1=0 odległość punktu S(4,−1) od prostej wynosi r=2

	|4a+1+4a−1|
d=		=2
	√a2+1

oblicz,

Patryk: to co napisałem ja Eta i ty teraz jest poprawne nie sugeruj się rysunkiem bo 1/4=0.25 a √15{15}≈0.25818...

Dominik: albo blad jest w odp, bo dla takich a punkt A rzeczywiscie nalezy do wyliczonych prostych. pomysl Ety na to zadanie to zreszta potwierdza.

Kipic: No odpowiedzi pewnie jak zwykle sa zryte Dziekuje Wszystkim za pomoc w tym zadaniu