Stereometria - Ostrosłup rock: Podstawą ostrosłupa ABCS jest trójkąt prostokątny o kacie prostym w wierzchołku C. Promień okręgu opisanego na tym trójkącie jest równy 3. Ściany boczne ACS i BCS są prostopadłe do podstawy. Pole ściany ABS jest równe 12√2 i jest ona nachylona do podstawy pod kątem 60 stopni. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.

rock: Nikt nie spróbuje?

rock: z

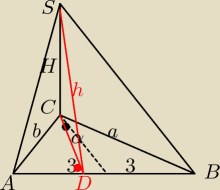
Mila: α=60^o Promień kręgu opisanego na Δprostokątnym jest równy połowie przeciwprostokątnej. |AB|=6 P_ΔABS=12√2

	1
PΔABS=		*|AB|*h
	2

1
	*6*h=12√2
2

h=4√2 W ΔDCS:

	H
sin60=		⇔H=sin60*4√2=2√6
	h

	CD		1		CD
cos60=		⇔		=		⇔CD=2√2
	h		2		4√2

Dokończysz? Masz odpowiedź?

rock: V=8√3, P=12+24√2 po pierwsze dzieki, do tego momentu sam doszedłem ale nie wiem jak obliczyć pole podstawy jakby przyjąć, że CD jest wysokością pola podstawy to wyjdzie ale ja jakoś sobie tego nie wyobrażam

Mila: CD jest wysokością podstawy, jak inaczej wyznaczyłbyś kąt α między płaszczyznami? SD⊥AB i CD⊥AB

Mila: Wszystko, ładnie wychodzi, chociaz trzeba pomysleć.

rock: ok dzieki

Mila: Zrobione?

rock: Ma jeszcze problem z polem

Mila: Problem z przyprostokątnymi?

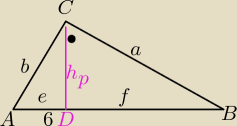
Mila: W Δ prostokątnym wysokość poprowadzona z wierzchołka kąta prostego jest równa h=√e*f⇔h²=e*f h_p=CD=2√2 (2√2)²=e*f⇔e*f=8 e+f=6 Załóżmy, że e<f f=6−e e(6−e)=8 e²−6e+8=0 e=2 lub e=4 Dla e=2 mamy f=4 b²=2²+(2√2)²⇔b²=4+8⇔b=2√3 a²=4²+(2√2)²⇔ dokończ

Bogdan: Już było niedawno, jest tu 188561

Mila: Do Bogdana, nie zauważyłam , że to już rozwiązane, zrezygnowałam z Twojego sposobu wyznaczenia długości przyprostokątnych, aby uniknąć pierwiastków z pierwiastków.