zadanie ze bioru maturalnego, stereometria
Wojtas: Podstawą ostrusłupa ABCS jest trójkąt prostokatny o kącie prostym w wierzchołku C. Promień
okręgu opisanego na tym trójkącie jest równy 3. Sciany boczne ACS i BCS są prostopadłe do
podstawy. Pole ściany ABS jest równe 12√2 i jest nachylona do podstawy pod kątem 60 stopni.
Oblicz objetość i pole powierzchni całkowitej graniastosłupa
23 lut 14:11
23 lut 14:33
Wojtas: wydaje mi sie że hs i hp nie koniecznie muszą sie zbiegać w jednym punkcie na odcinku AB, mam
racje?
23 lut 14:40
dero2005:
muszą się zbiegać (spotykać) w jednym punkcie gdyż inaczej nie byłoby kąta α gdzie odmierzyć
23 lut 14:43
dero2005:
płaszczyzna hp, hs, h jest prostopadła do podstawy ABC i do boku ABS
23 lut 14:46
Mati_gg9225535:
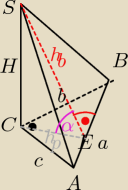 Dane: Szukane:
Dane: Szukane:
R=3 V = ?
α = 60
o P
c = ?
P
ΔABS = 12
√2
ΔABC:
ΔABS:
| | 1 | |
12√2 = |
| * 6 * hb ⇒ hb = 4√2 |
| | 2 | |
ΔCES:
α=60
o
ΔABC:
| | 1 | | 1 | |
PΔABC = |
| *a * hp = |
| * 6 * 2√2 = 6√2 |
| | 2 | | 2 | |
a)
| | 1 | | 1 | |
V = |
| * PΔABC * H = |
| * 6√2 * 2√6 = 8√3 |
| | 3 | | 3 | |
a
2 = b
2 + c
2
c
4 − 36c
2 + 288 = 0
t = c
2
t
2 − 36t + 288 = 0
Δ = 1296 − 1152 = 144
√Δ = 12
| | 36 − 12 | | 36+12 | |
t = |
| v t = |
| |
| | 2 | | 2 | |
t = 12 v t = 24
c
2 = 12 v c
2 = 24
c
1 = 2
√3 v c
2 = 2
√6
| | 12√2 | | 12√2 | |
b1 = |
| b2 = |
| |
| | 2√3 | | 2√6 | |
v
| | ⎧ | b = 2√6 | |
| przyjmujemy, że | ⎩ | c = 2√3 |
|
b)
| | c * H | | 2√3 * 2√6 | |
PΔACS = |
| = |
| = 6√2 |
| | 2 | | 2 | |
| | b * H | | 2√6 * 2√6 | |
PΔBCS = |
| = |
| = 24 |
| | 2 | | 2 | |
P
c = P
ΔABC + P
ABS + P
ΔACS + P
ΔBCS
P
c = 6
√2 + 12
√2 + 6
√2 + 24 = 24 (1 +
√2)
23 lut 14:55
Mati_gg9225535: uffff

23 lut 14:56
Mati_gg9225535: moglem sie gdzies pomylic

23 lut 14:57
Wojtas: wy zakładacie że te wysokości hp i hs sie przecinają, tak nie jest
to nie jest ostrosłup prawidłowy
23 lut 14:58
dero2005:
uruchom wyobraźnię przestrzenną
23 lut 15:01
Wojtas: w takim razie zawsze w ostrosłupie kąt nachylenia ściany do podstawy to kąt miedzy
wysokościami?
23 lut 15:06
dero2005:
tak
23 lut 15:08
Bogdan:
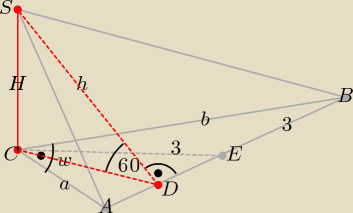
UWAGA: Odcinek ES nie jest wysokością trójkąta ABS
| | 1 | |
c = |AB| = 6, |
| *6*h = 12√2 ⇒ h = 4√2 |
| | 2 | |
Korzystając z własności trójkąta prostokątnego o kącie ostrym 60
o otrzymujemy:
| | 1 | |
w = |
| h = 2√2 oraz H = w√3 = 2√6 |
| | 2 | |
| | 1 | |
Pole podstawy ostrosłupa Pp = |
| *6*w = 3*2√2 = 6√2 |
| | 2 | |
| | 1 | |
Objętość ostrosłupa: V = |
| * 6√2 * 2√6 = 8√3 |
| | 3 | |
| | 1 | | 1 | | 1 | |
Pc = Pp + PABS + |
| a*H + |
| b*H = 6√2 + 12√2 + |
| *2√3(a + b) = |
| | 2 | | 2 | | 2 | |
= 18
√2 +
√3(a + b)
Trzeba obliczyć wartość a+b.
| | 1 | | 1 | |
a2 + b2 = 36, Pp = |
| ab ⇒ 6√2 = |
| ab /*4 ⇒ 24√2 = 2ab |
| | 2 | | 2 | |
(a + b)
2 = a
2 + 2ab + b
2 ⇒ a + b =
√36 + 24√2 = 2
√9 + 6√2
P
c = 18
√2 +
√3*2
√9 + 6√2 = 18
√2 + 2
√27 + 18√2 = 18
√2 + 2
√ (3√2+3)2 =
= 18
√2 + 2*|3
√2+3| = 18
√2 + 6
√2 + 6 = 24
√2 + 6
23 lut 21:20
Matematyk bez szkoły: Mógłby mi ktoś wytłumaczyć jedną rzecz?
Skoro u Bogdana H wyszło 2√6, to czemu przy wyliczaniu Pola całkowitego podstawia za H 2√3?
Zresztą i tak wynik Pc różni się (no chyba, że jest źle w odpowiedziach, ponieważ powinno być
według tego 12(1 + 2√2) = 24√2 + 12, a u Bogdana wyszedł wynik za mały o 6.
24 paź 12:27
Matematyk bez szkoły: bump
24 paź 15:56
Lukasz: @Mati
gg9225535: jedyny błąd to w 3 linijce od dołu

2
√6 * 2
√6 *
12 =
242 = 12
Ppc ⇒ 12(1+2
√2)
Pozdrawiam, i dzięki za pokazanie sposobu na 2 część zadania

4 cze 21:48
jaros: Właśnie ktoś wie dlaczego u Bogdana H = 2
√6 a potem H = 2
√3 
4 cze 22:03
ICSP: zawsze jest H = 2√6.
On podstawia później wartość w a nie H.
4 cze 22:04
jaros: | | 1 | | 1 | |
Jak to "w" przecież widać tam, że jest |
| *b*H = |
| * 2√3 |
| | 2 | | 2 | |
4 cze 22:07
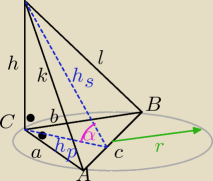 185228
185228
 Dane: Szukane:
R=3 V = ?
α = 60o Pc = ?
PΔABS = 12√2
ΔABC:
Dane: Szukane:
R=3 V = ?
α = 60o Pc = ?
PΔABS = 12√2
ΔABC:


 UWAGA: Odcinek ES nie jest wysokością trójkąta ABS
UWAGA: Odcinek ES nie jest wysokością trójkąta ABS
 2√6 * 2√6 * 12 = 242 = 12
Ppc ⇒ 12(1+2√2)
Pozdrawiam, i dzięki za pokazanie sposobu na 2 część zadania
2√6 * 2√6 * 12 = 242 = 12
Ppc ⇒ 12(1+2√2)
Pozdrawiam, i dzięki za pokazanie sposobu na 2 część zadania 
