prosze o pomoc koniiiiiczynka: Pole trapezu równoramiennego opisanego na okręgu jest równe 72 √3 Oblicz długości podstaw tego trapezu, wiedząc, że jego ramię jest nachylone do podstawy pod kątem 60 stopni

stanisław: https://matematykaszkolna.pl/forum/38496.html

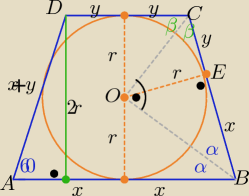
Eta: |AB|=2x , |DC|=2y , x, y >0

2r		√3
	=sin60o=		⇒ 4r=(x+y)*√3
x+y		2

	2x+2y
P(tr)=		*h= (x+y)*2r= 8r2√3
	2

8r²√3= 72√3 ⇒ r²=27 ⇒ r=3√3 trójkąt BOC jest prostokątny o kątach 30^oi 60^o ( dlaczego? ..odpowiedź zostawiam dla Ciebie

	4r
to: r2=x*y ⇒ x*y= 27 i (x+y)=		⇒ x+y= 12
	√3

x+y=12 x*y=27 to x=9 i y=3 |AB|= 2x=.... |DC|=2y=....

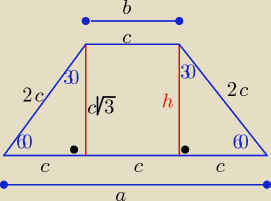
Eta: Jak się jest zdrowszym(po grypie) to i mózg lepiej pracuje 2 sposób ( najprostszy) 2c −−− długość ramion trapezu , c>0 a, b −−− długości podstaw a,b>0

	a+b
Z warunku opisania trapezu na okręgu: a+b=2c+2c =4c ⇒		= 2c
	2

Korzystamy z własności trójkąta prostokątnego o kątach 30^o, 60^o h= c√3

	a+b
P(trapezu)=		*h = 2c*c√3
	2

2c²√3= 72√3 ⇒ c²=36 ⇒ c=6 zatem długości podstaw trapezu to: a= 3c = 18 i b= c=6