trygonometria Kipic: to jest chyba jakis joke Wyznacz liczbe dodatnich rozwiazan rownania 1−lx−4l=2sinm w zaleznosci od parametru m .

	1
i terz wedlug ksiazki powinienenm zobaczyc ze sinm nie ma rozwiazan gdy sinm>		? jak mam
	2

to zobaczyc prosze o wyjasnienie bo nie ogarnam wogule

krystek: w ogóle Ix−4I=2sinm−1 i teraz 2sinm−1>0

Kipic: czyli ta wartosc bezwzgledna tak jakby znika ?

krystek: ups nie ma rozwiązania Źle przekształciłam Ix−4I=−2sinx+1 −2sinm+1<0 sinm>

Kipic: nie chyab wczesniej bylo dobrze ? to 2sinm−1>0 czyli sinm>U{1} bo to zadanie mam z takimi podpunktami jak robic i tam wlasnie jest ze sinm>

	1
	2

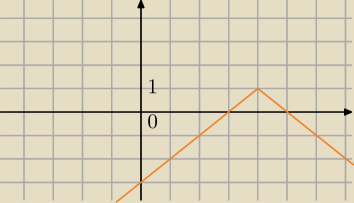
Mila: f(x)=1−|x−4| y=2sin(m) 2sin(m)=0 lub .. dokończę za 2 godziny, mam gościa, albo sam dokończ

Kipic: raczej sam tego zadania nie ogarne wiec poczekam

Kipic: level up

Eta: https://matematykaszkolna.pl/forum/138530.html Kliknij , bo chce mi się pisać

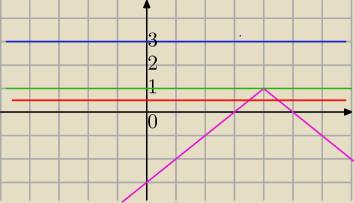
Mila: 1) 2sin(m)>1 brak rozwiązań,( przykład niebieskiej prostej)

	1		π		5π
sin(m)>		⇔m∊(		+2kπ;		+2kπ) brak rozwiązań.
	2		6		6

2)

	1
2sin(m)=1 jedno rozwiązanie ⇔sin(m)=		⇔( zielona prosta)
	2

	π		5π
m=		+2kπ lub m=		+2kπ
	6		6

Trzeba zbadać czy rozwiązanie jest dodatnie f(x)=1−|x−4| 1−|x−4|=1⇔|x−4|=0⇔x=4>0

	1
3) 2sin(m)<1⇔sin(m)<		i 2sin(m)>0
	2

	π		5π
m∊(0+2kπ;		+2kπ) lub m∊(		+2kπ);π+2kπ)
	6		6

Napisz, czy zgadza się z odpowiedzią.

Kipic: jawol Mila jak zawsze dobrze i to wszystkie podpunkty wedlug oceniania Dziekuje

Mila: