Trygonometria
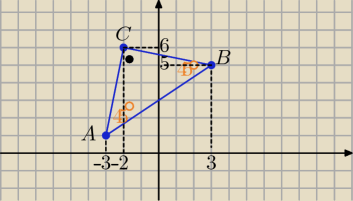
Kasia: Wierzchołki trójkąta ABC mają współrzędne A(−3,1), B(3,5) oraz C(−2.6)
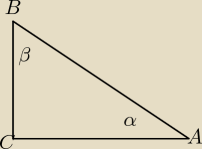
a) wykaż że trójkąt ABC jest prostokątny
b) Oblicz wartość wyrażenia (sinα + sinβ)−1 , gdzie α,β − miary kątów ostrych trójkąta ABC
Obliczyłam że:
|AB|=√52
|BC|=√27
|AC|=√25
Później z Pitagorasa wychodzi że:
25+27=52
52=52
L=P
A więc trójkąt jest prostokątny
Ale jak zrobić punkt b? Proszę o pomoc.
22 lut 19:21
PW: To nie jest twierdzenie Pitagorasa!
b) Zastosować definicje − co to jest sinα i sinβ
22 lut 19:38
Kasia: To z jakiego twierdzenia to zrobić?
b)
sinα=√25/√52
sinβ=√27/√52
i co dalej?
22 lut 19:40
PuRXUTM: w pierwszym Kasiu ja bym sobie narysował układ współrzędnych naniósł bym punkty i później
wyznaczył równania prostych pr.AC i pr. BC i udowodniłbym że są one prostopadłe ze wzoru że
iloczyn współczynników kierunkowych jest równy −1
https://matematykaszkolna.pl/strona/42.html
22 lut 19:41
PuRXUTM: to jest twierdzenie odwrotne do twierdzenia pitagorasa, i tak możesz moim zdaniem to zrobić
22 lut 19:42
krystek:
22 lut 19:44
PuRXUTM: sinα=cosβ w tym przypadku
22 lut 19:45
krystek: Ale Kasia dobrze zrobiła Wykazał z Pitagorasa
22 lut 19:47
Kasia: | | √27 | |
to sinα= |
| ?  |
| | √52 | |
22 lut 19:50
PW: Tak zrobić jak zrobiłaś, tyle że zastosowałaś
twierdzenie odwrotne do twierdzenia
Pitagorasa.
Twierdzenie Pitagorasa mówi o związku między bokami w trójkącie prostokątnym:
jeżeli trójkąt jest prostokątny, to długości boków spełniają związek a
2+b
2=c
2 (przy
odpowiednich oznaczeniach).
− dodać te dwie liczby i odjąć jedynkę − zgodnie z poleceniem.
22 lut 19:51
krystek: Tak
22 lut 19:51
Kasia: Ta jedynka oznacza do potęgi minus pierwszej

| | √27 | | √25 | | 3√3 | | 5 | |
( |
| + |
| ) do potęgi minus pierwszej=( |
| + |
| ) |
| | √52 | | √52 | | 2√13 | | 2√13 | |
do potęgi minus pierwszej
I nie umiem dalej

22 lut 19:59
krystek: | | 1 | |
a−1= |
| czyli odwrotnośc ułamka |
| | a | |
22 lut 20:01
22 lut 20:04
Kasia: to:
i co dalej? Wspólny mianownik?
22 lut 20:06
Kasia: | | 3√3+5 | |
( |
| ) do minus 1 i jak to policzyć? |
| | 2√13 | |
22 lut 20:08
22 lut 20:18
krystek: Usuń niewymiernośc z mianownika mnożąc L i M przez (3√3−5)
22 lut 20:22
krystek: | 2√13*(3√3−5) | |
| =.. i dalej dasz rade |
| 9*3−25 | |
22 lut 20:24
22 lut 20:27
krystek: Dobrze policzyłas dł boków , nie sprawdzałam.Teraz film , Pa pa
22 lut 20:31
Kasia: papa

Może ktoś mi pomóc z tym przykładem, proszę!

22 lut 20:36
Beti: no więc tak:
1) źle policzyłaś długości boków trójkąta

powinno być:
|AB| =
√52 −−> i to było dobrze
|BC| =
√26
|AC| =
√26
2) teraz spróbuj policzyć te sin i cos −− powinno już wyjść dobrze

22 lut 20:42
Kasia: Faktycznie jej tak to jest jak się robi zadania w piątek wieczorem

Wyszło mi tak:
Po usunięciu niewymierności:
Ale mam pytanko tu usuwam wymierność mnożąc przez 2
√26 a nie przez sam
√26?
22 lut 20:52
Beti: oczywiście, że przez sam
√26
jednak, jeśli pomnożysz przez cały mianownik, czyli 2
√26, to też otrzymasz dobry wynik, tylko
więcej sie naliczysz

22 lut 20:54
Kasia: aha dziękuję, zawsze miałam w takich przypadkach wątpliwość

A dlaczego gdy sprawdzam czy trójkąt jest prostokątny używam tw. odwrotnego do tw. Pitagorasa?
Jaka to jest różnica?

22 lut 20:56
Beti: w tw. Pitagorasa założeniem jest, że trójkąt jest prostokątny, a wtedy zachodzi zależność
a2+b2 = c2 (mówiąc w dużym skrócie).
Tw. odwrotne do Pitagorasa jest, jak sama nazwa wskazuje, odwrotne, czyli założeniem jest
zależność a2 + b2 = c2. Jeśli boki trójkąta spełniaja tą zależnośc, to wtedy trójkąt jest
prostokątny.
Tyle
22 lut 21:01
Kasia: Aha czyli wzór jest taki sam, tylko opis słowny jest odwrotny?
22 lut 21:06
Beti: To tak jak jazda z Poznania do Warszawy i odwrotnie. Stacje końcowe te same, ale podróż jednak
odbywa się w przeciwnych kierunkach.

22 lut 21:13
Kasia: Rozumiem, bardzo dziękuję

22 lut 21:29
Beti: na zdrowie

22 lut 21:36
Eta:
| | 1 | | √2 | |
(sinα+sinβ)−1 = (√2)−1= |
| = |
| |
| | √2 | | 2 | |
22 lut 21:40
Kasia: Również bardzo dziękuję

22 lut 21:49





 Może ktoś mi pomóc z tym przykładem, proszę!
Może ktoś mi pomóc z tym przykładem, proszę!
 powinno być:
|AB| = √52 −−> i to było dobrze
|BC| = √26
|AC| = √26
2) teraz spróbuj policzyć te sin i cos −− powinno już wyjść dobrze
powinno być:
|AB| = √52 −−> i to było dobrze
|BC| = √26
|AC| = √26
2) teraz spróbuj policzyć te sin i cos −− powinno już wyjść dobrze 
 Wyszło mi tak:
Wyszło mi tak:


 A dlaczego gdy sprawdzam czy trójkąt jest prostokątny używam tw. odwrotnego do tw. Pitagorasa?
Jaka to jest różnica?
A dlaczego gdy sprawdzam czy trójkąt jest prostokątny używam tw. odwrotnego do tw. Pitagorasa?
Jaka to jest różnica? 




