trójkąt olka:

	3
a to W trójkącie prostokątnym sinus jednego z kątów jest równy		. Promień okręgu
	5

wpisanego w ten trójkąt ma długość 7 cm. oblicz pole tego trójkąta.

evil_woodworm: P−pole trójkąta Obw.−obwód trójkąta 2P r= −−−−−− Obw. Ja z tego policzyłam, ale nie wiem, czy to dobra metoda Odp.P=294cm²

olka: czy ktoś ma jeszcze jakiś pomysł?

evil_woodworm: To chyba jednak chodzi o tą metodę jak tak poszperałam szukając czegoś innego. Rozumiesz ją, czy nie bardzo?

olka: nie rozumiem

evil_woodworm: juz tłumaczę

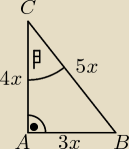evil_woodworm: Więc, stosunek przyprostokątnej naprzeciwko kąta (nazwijmy go β) do przeciwprostokątnej jest rowny 3:5. Nazwijmy bok, którego nie znamy m, więc z tw.Pitagorasa: m²+3²=5² m²=16 m=4 Ale, że to jest tylko stosunek długości boków, dodaję x do każdej długości (jak na rysunku). Teraz mamy wzór.

	2P
r=
	Obw

r−promień okręgu wpisanego P−pole trójkąta Obw−obwód trójkąta Podstawiamy do wzoru to co mamy:

	1   2* *4x*3x   2
7=
	4x+5x+3x

z czego wychodzi:

	12x2
7=
	12x

A po skróceniu: 7=x Teraz wystarczy wymnożyć boki: |AB|=3x=3*7=21 |CA|=4x=4*7=28

	1
P=		*28*21
	2

P=294 [cm²] Rozumiesz? Jak nie, to pytaj

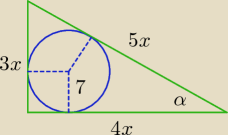Bogdan: Długość r promienia okręgu wpisanego w trójkąt prostokątny o przyprostokątnych a, b i przeciwprostokątnej c można wyznaczyć z zależności: 2r = a + b − c W tym zadaniu: 2*7 = 3x + 4x − 5x ⇒ 14 = 2x ⇒ x = 7, a = 3x = 21, b = 4x = 28, c = 5x = 35.

	1		1
Pole trójkąta P =		(a + b + c)*r ⇒ P =		(21 + 28 + 35) * 7 = 294.
	2		2

evil_woodworm: No tak, było do przewidzenia, że jest jakaś prostsza zależność z której można to policzyć, a ja jak zwykle naokoło...−.− Ale dzięki Bogdan, bo nie znałam (albo nie pamietałam^^') tego

Eta: Witam podam inną wersję rozwiązania; dla trójką prostokątnego (**) 2r= a+b −c , gdzie 2r −−− średnica okregu wpisanego w ten trójkąt z treści zad. mamy : ^a_c= ³₅ => a= ³₅*c to: b= ⁴₅*c zatem z (**)mamy : ³₅*c + ⁴₅*c − c = 2*7 ²₅*c= 14 => c= 35 to a= ³₅*35 = 21 i b= ⁴₅*35 = 28

	a*b
PΔ=		... policz
	2

odp. taka jak podała evil

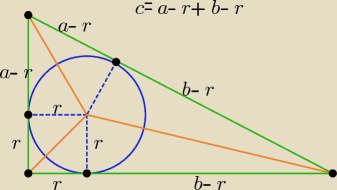Bogdan: c = a − r + b − r ⇒ 2r = a + b − c

olka: rozumiem ale sama bym na to nigdy nie wpadła... Dziękuje Wam

fifi: <(")