trtygonometria
andrzej: Witam moglby mi ktos pomoc rozpisac tę funkcję:
f(x)=|sinx| − sinx dla xE <−2π,2π>
i g(x)=f(|x|) dla tej samej dziedziny....tę f(x) potrafie ale nie wiem juz jak z tym f(|x|)
12 lut 16:45
andrzej: w sumie to oby dwie nie wiem jak

12 lut 16:47
12 lut 18:33
MQ: Podpowiedź:
Kiedy sinx jest dodatnie, to |sinx|=sinx, więc f(x)=sinx − sinx
Kiedy sinx jest ujemne, to |sinx|=−sinx, więc f(x)=−sinx−sinx
12 lut 18:37
andrzej: no to wiem to rozpisalem ze
|sinx| = {sinx dla xe <−2π,−π> u <0,π>
−sinx dla xe (−π,0) u (π,2π) }
ale teraz nie wiem co dalej
12 lut 20:02
krystek: f(x)=0 tam gdzie sinx>0
f(x)=−2sinx tam gdzie sinx<0
12 lut 20:06
andrzej: no to wiem
ale teraz jak zrobic g(x)=f(|x|)
12 lut 20:06
krystek: f(IxI) kreślisz f(x) i dla x<0 odbijasz wartośc dla x>0 ( częśc dla ujemnych "znika")
12 lut 20:09
Mila:
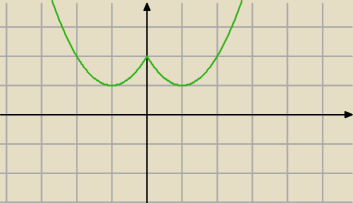
Przykład do komentarza Krystek:
y=x
2−2|x|+2 z zielony
12 lut 20:44
Mila:
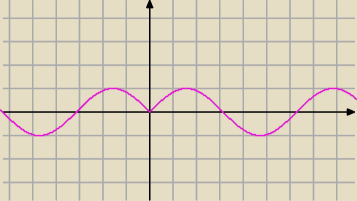
y=sin|x|
12 lut 20:46
andrzej: ale to tylko odobija sie dla x<0?
12 lut 20:51
Mila: Tak, wykresem dla x<0 nie zajmujesz się (pomijasz, jeśli x=−1 to |−1|=1, czyli masz
f(|−1|)=f(1)
12 lut 20:54
andrzej: to jak bedzie wygladal wykres f(|x|)=|sin|x|| − sin|X|
x{−2pi, −pi> lub <o,pi> = 0
x (−pi,0) u (pi,2pi) = −2sin|x|



?
12 lut 21:09
MQ: No, przecież ci już napisali.
Rysujesz funkcję tylko dla x>0 i odbijasz rysunek symetrycznie wzgl. osi OY.
12 lut 21:12
Mila:
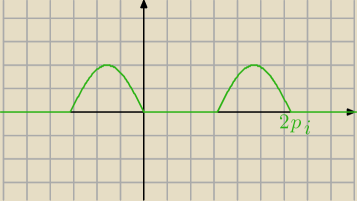
1) y=|sin(x)|−sin(x)
x∊<0;π> to f(x)=0
x∊(π;2π> to f(x)=2sinx
Na drugim będzie
g(x)=|sin(|x|)|−sin(|x|)
12 lut 21:17
Mila:
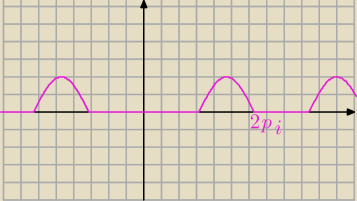
g(x)=|sin(|x|)|−sin(|x|)
12 lut 21:20
asian: tzn ze funckja parzysta jak symetryczna do y?
12 lut 22:13
12 lut 22:14




 Przykład do komentarza Krystek:
y=x2−2|x|+2 z zielony
Przykład do komentarza Krystek:
y=x2−2|x|+2 z zielony
 y=sin|x|
y=sin|x|


 ?
?
 1) y=|sin(x)|−sin(x)
x∊<0;π> to f(x)=0
x∊(π;2π> to f(x)=2sinx
Na drugim będzie
g(x)=|sin(|x|)|−sin(|x|)
1) y=|sin(x)|−sin(x)
x∊<0;π> to f(x)=0
x∊(π;2π> to f(x)=2sinx
Na drugim będzie
g(x)=|sin(|x|)|−sin(|x|)
 g(x)=|sin(|x|)|−sin(|x|)
g(x)=|sin(|x|)|−sin(|x|)